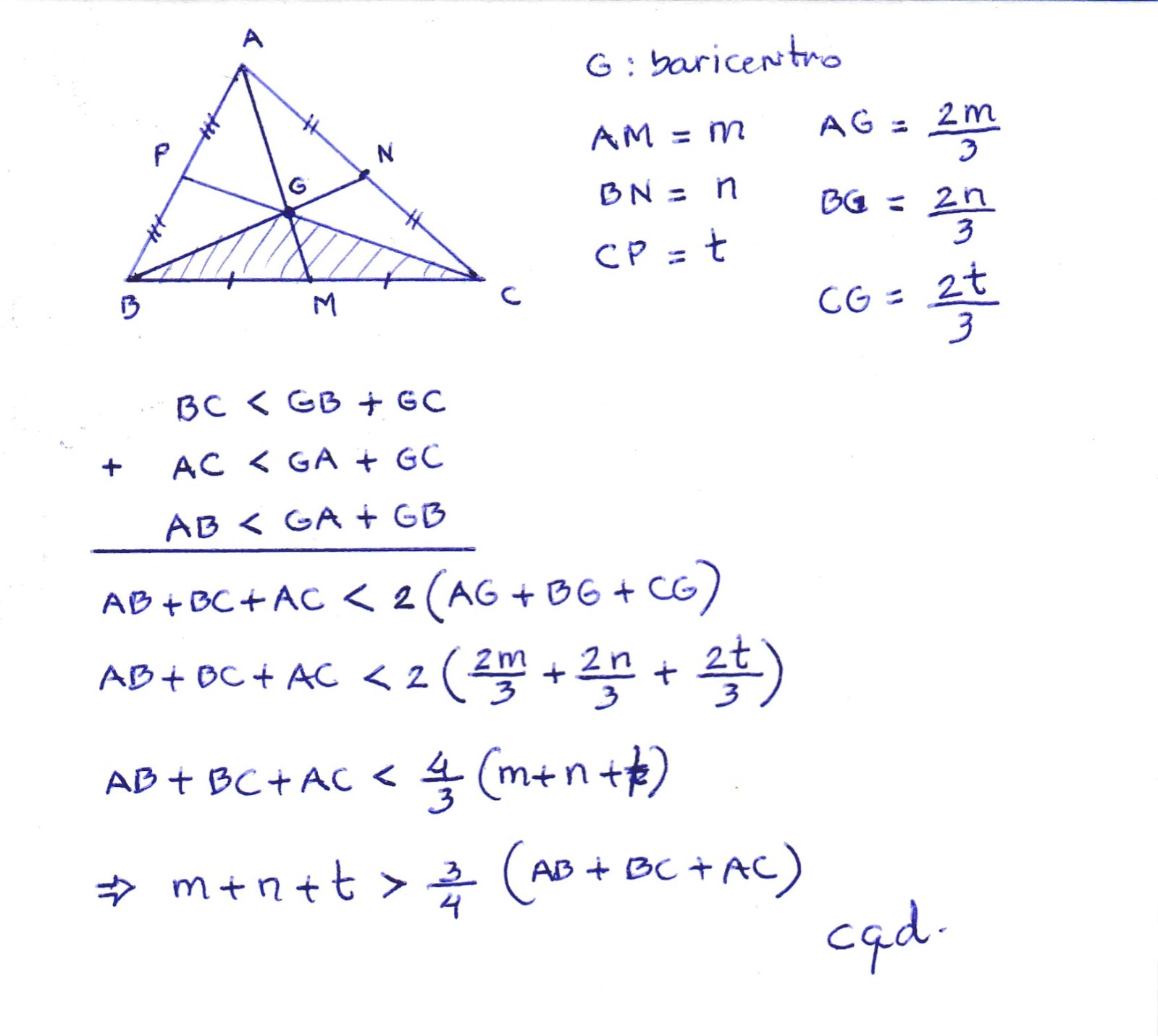
Soma das medianas de um triângulo > 3/4 de seu perímetro?

por Arcanjo M Seg 07 Mar 2011, 12:56

Prove que a soma das medianas de um triângulo é maior do que 3/4 de seu perímetro.

por Jeffson Souza Qui 17 Mar 2011, 21:43

Bom amigo é o seguinte ,vamos ver se esse seu enunciado tem algum erro.

Seja AM ,CZ e BX as Medianas.

BM+AM>AB

AM>AB-BM

Por outro lado temos,

AM+MC>AC

AM>AC-MC

Somando as duas teremos:

2AM>AB+AC-BM-MC

2AM>AB+AC-(BM+MC)

2AM>AB+AC-BC

Analogamente :2BX>AB+BC-AC e 2CZ>AC+BC-AB

Somando

2AM+2BX+2CZ>AC+BC+AB

AM+BX+CZ>(AC+BC+AB)/2

AM+BX+CZ>1/2(AC+BC+AB)

As somas das medianas são maiores que o semi perímetro do triângulo.

Bom agora vamos analisar o seguinte:

Pela desigualdade triangular aplicada aos triângulos ABM e ACM, respectivamente AM-BM < AB e AM-MC < AC

Somando obteremos 2AM-(BM+MC) < AB+AC

2AM<(AB+AC+BC)

AM<(AB+AC+BC)/2

Analogamente

CZ<(AB+AC+BC)/2

Bx<(AB+AC+BC)/2

AM+BX+CZ<3/2(AB+AC+BC)

Comprovando que o enunciado esta errado!

Por favor verifique

Very Happy

por Arcanjo M Sex 18 Mar 2011, 20:29

EU MESMO NÃO SEI A RESPOSTA. ESSA (A SEGUIR) FOI DE UM OUTRO FÓRUM DE DISCUSSÃO:

"Tomando como exemplo um triângulo equilátero de lado 8 cm:
Seu perímetro será = 24cm.
Entao:
24.3/4 = 18cm.

Cada mediana irá de cada vertice a metade do lado oposto.
Ou seja, ira cortar o outro lado em 4cm.
Suponha que mediana seja m:

m²=4²+8²
m²=16+64=80
m=√80
m=9 aproximadamente

Entao somando as medianas teremos aproximadamente 27cm.

Então a soma das medianas é maior que 3/4 do perímetro deste triângulo.

27cm > 18cm. "

O QUE ACHA? ESTÁ CERTO?

OBRIGADO!

por **Elcioschin** Sáb 19 Mar 2011, 12:40

Arcanjo

Para a demonstração ser válida, ela deve abranger QUALQUER triângulo.
Assim, este outro fórum provou APENAS que num triângulo equilátero a afirmação é verdadeira.

por **luiseduardo** Sáb 19 Mar 2011, 12:42

Elcioschin escreveu:Arcanjo

Para a demonstração ser válida, ela deve abranger QUALQUER triângulo.
Assim, este outro fórum provou APENAS que num triângulo equilátero a afirmação é verdadeira.

Élcio, acho que nem isso kkkk
Pois no caso, ele ainda colocou um valor fixo para o lado, então, a prova ficaria limitada a um triângulo equilátero de lado 8 cm.

por Jeffson Souza Sáb 19 Mar 2011, 13:41

Olá Arcanjo M.

Na minha resolução as medianas estão no seguinte intervalos:

AM+BX+CZ>1/2(AC+BC+AB)
AM+BX+CZ<3/2(AB+AC+BC)

1/2(AC+BC+AB) < AM+BX+CZ < 3/2(AB+AC+BC)

Observe que (AC+BC+AB) é o perímetro do triângulo.

0,5(AC+BC+AB) < AM+BX+CZ < 1,5(AB+AC+BC)

3/4=0,75

A unica coisa que eu posso afirmar é:

As somas das medianas são maiores que o semi perímetro do triângulo.
As somas das medianas são menores que 3/2 do seu perímetro.