Valor de n - Logaritmo

Para testar um novo antibiótico, um laboratório farmacêutico deixou uma cultura bacteriana se desenvolver durante n horas, durante as quais a população de bactérias triplicou a cada 2 horas. Em seguida, foi aplicado o antibiótico, que fez com que a população diminuísse a uma taxa de 25% a cada hora durante as 10 horas seguintes, até voltar ao nível inicial. Usando-se  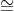 1,26, se necessário, pode-se concluir que o valor de n é

A) 0,09
B) 2,6
C) 4,3
D) 5,2
E) 7,8

valeriasjs escreveu:Para testar um novo antibiótico, um laboratório farmacêutico deixou uma cultura bacteriana se desenvolver durante n horas, durante as quais a população de bactérias triplicou a cada 2 horas. Em seguida, foi aplicado o antibiótico, que fez com que a população diminuísse a uma taxa de 25% a cada hora durante as 10 horas seguintes, até voltar ao nível inicial. Usando-se   1,26, se necessário, pode-se concluir que o valor de n é

A) 0,09
B) 2,6
C) 4,3
D) 5,2
E) 7,8

Boa noite, Valéria.

x = quantidade inicial de bactérias

Primeiras n horas:
x, 3x, 3².x, 3³.x, ...

Lembrando que entre cada termo da sequência acima existe a distância de 2 horas, então, após n horas a ordem do último termo deverá ser:
n/2 + 1 = expoente da base 3
onde n é a ordem do termo na sequência, a saber:
n(x) = 1
n(3x) = 2
etc.

Usando a sequência supra para conferir:
n/2 + 1 = 4/2 + 1 = 2 + 1 = 3 (veja que o expoente do 4° termo (n=4) é mesmo =3)

Assim sendo, o último termo da sequência, ao fim das n horas, dever ser igual a:
an = a1.q^(n - 1) (das fórmulas de PG)
an = x . 3^(n/2+1 - 1)
an = 3^(n/2).x

Este enésimo termo da 1ª parte da questão será o 1° termo da segunda parte.
A razão entre os termos na 2ª parte será igual a 0,75 (=100% - 25%), que converteremos na fração ordinária 3/4:

3^(n/2).x ; (3/4).3^(n/2).x ; (3/4)².3^(n/2).x ; ... ; (3/4)¹º.3^(n/2).x

O valor do último termo desta 2ª sequência é igual à quantidade inicial de bactérias, ou seja, igual a x; portanto, fica:

(3/4)¹º * 3^(n/2).x  = x

Dividindo toda esta equação por x, resulta em:

(3/4)¹º * 3^(n/2) = 1

Passando para logaritmos, vem:

10(log3 - 2log2) + (n/2)log3 = log1 = 0

(n/2)log3 = –10(log3 - 2log2)

O cálculo do valor deste segundo membro é

1,249387

aproximadamente 1,25; continuando, fica:

(n/2)log3 = 1,25
n/2 = 1,25/0,48
n = 2*1,25/0,48
n = 5,208...
n ≈ 5,2

Alternativa (D)



Um abraço.

Obrigada Ivo!!! Ajudou muito! Abraço!