Indução - Desigualdade das médias

Nesse link tem a prova por indução de ma ≥ mg: (também é do POTI)
http://poti.obmep.org.br/upload/Aula%2001%20-%20Desigualdades_1.pdf

Achei as provas bem "rotineiras". Pela vídeo-aula que dão, uma maneira de provar é através de logaritmo:

Tem-se então que o logaritmo da média geométrica é a media aritmética dos logaritmos dos números que compõem a média.
Temos o gráfico da função  :

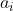Sendo  e 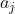 o menor e o maior termo da média, respectivamente, e  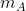a média aritmética; tem-se então que a média aritmética dos logaritmos pertencerá à região entre segmento que une os pontos  e  e a função f(x), isto é, a região sombreada:




Já a logarítmo da média aritmética não pertencerá ao segmento, pertencerá à função. E por isto, tem-se que:


Até aqui tudo bem, contudo, eu acho que não está tão bem definido ainda o porquê de a média geométrica pertencer à região sombreada. Teria alguma maneira de provar porque o limite inferior é o segmento que une os pontos  e

Quanto a este método, seria válida a resposta para correção? Ou há alguma falha, ou não poderia ser considerada para correção?

Olá!
Gostei bastante da demonstração acima, mas também não consegui entender completamente a parte que menciona a região sombreada...
Talvez, ela esteja relacionada com a desigualdade de Jensen, cuja demonstração não é do meu conhecimento. 
Des. de Jensen:
Se f é uma função côncava, então:
f([a1+a2+...an]/n)>/[f(a1)+f(a2)+...f(an)]/n
Segue o link com um material da OBM que contém a demo. da des. de Jensen:
https://www.google.com.br/url?sa=t&rct=j&q=&esrc=s&source=web&cd=2&cad=rja&uact=8&ved=0CCUQFjAB&url=http%3A%2F%2Fwww.obm.org.br%2Fexport%2Fsites%2Fdefault%2Frevista_eureka%2Fdocs%2Fartigos%2Fdesigualdades.doc&ei=SCC3VM-hBpLIsAST_4GQCw&usg=AFQjCNEpUHr1GNfgJh9V5Zx2ebJGgzJ03A&bvm=bv.83640239,d.cWc

Como o método utilizado difere da demonstração através do princípio da indução, acho que ele não seria válido para correção.

Quanto maior o logaritmando maior o logaritmo, então se
log_b (MA) ≥ log_b (MG) segue que MA ≥ MG.
A média de uma sequência de números sempre está entre o maior e o menor deles, nesse caso entre a_i e a_j, ou seja, qualquer média de a_k's estará entre a função e aquele segmento pois a_i é o menor valor possível e a_j o maior.

 Lembre-se que

A_K ' = log_b (A_K)
Não sei se respondi diretamente à sua dúvida, mas acho que é isso que queria saber.

Eu tive um raciocínio semelhante ao seu. Pra provar que MA >= MG, basta provar que log MA >= log MG. Ou seja, log MA >= MA (log a1, log a2, ..., log an)
Concordemos que o baricentro de um polígono está sempre no interior do polígono.
Em um triângulo de vértices A=(x1, y1), B=(x2, y2) e C=(x3, y3), tem-se que o baricentro é calculado por G=((x1+x2+x3)/3;   (y1+y2+y3)/3). Se for um quadrilátero, é calculado por ((x1+x2+x3+x4)/4,   (y1+y2+y3+y4)/4 ). Ou seja, a média aritmética dos X, e a média aritmética dos Y.
Se os pontos forem 
Então o baricentro será:

Ou seja:

Um exemplo é o abaixo.

Contudo, ainda não sei se este método serve para provar a desigualdade. Por exemplo, pra provar que raiz de 2 é irracional, não é necessário utilizar o princípio de indução. Além de outras demonstrações.
Por indução seria uma certeza, mas se esse método servir, então o princípio de indução faz-se opcional.