questão mdc (semelhante a anterior )

calcular o menor número que , dividido por 15 e 18 , deixa sempre o mesmo resto 12 .

Olá, Erick

Peguemos, por exemplo, 28:13 ----> resto = 2
Se você subtrair o dividendo (28) pelo resto (2), encontraremos 26, que é divisível por 13

Aplicando tal propriedade:

x:15 ----> resto = 12
x:18 ---> resto = 12

---> (x - 12) : 15 ---> resto = 0
---> (x - 12) : 18 ---> resto = 0

Ele quer o menor x possível; logo, (x-12) é o MMC entre 15 e 18. MMC (15,18) = 90. Então:
x - 12 = 90 ---> x = 102

olá hoshiminiag , então o cerne dessa questão é sempre achar um número que subtraído do resto doze sempre resultando num numero divisivel por 15 e 18 . nossa é bem diferente essa questão , aonde tu aprendeu essas paradas cara ? rsrsrs

Exato, Erick.
É uma simples propriedade: (Dividendo - Resto) dividido pelo (divisor) ---> resto 0

não sabia desa propriedade

desculpe estava observando a propriedade e fiquei com uma pergunta porque o resto tem que ser zero ?

Todo número, quando dividido por outro deixa um resto que varia desde 0 até d. Exemplo:

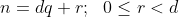
neste caso, a divisão é essa:

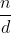
quando dividido obtém-se o resultado q, e o resto chamado de r. Deste modo, se deixa um resto, se tirarmos esse resto, n será multiplo de d. Ou seja:


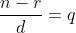
No exemplo acima, temos que n é o número que queremos descobrir, d é 15 e 18, e r vale 12. Logo:

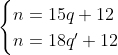
Assim, manipulação algebricas você descobre que n-r é multiplo de 15 e 18 ao mesmo tempo:

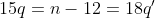
Assim, para achar os números q e q', temos que eles deverão ser pequenos, e q deve ser multiplo de 6, e q' deve ser multiplo de 5:

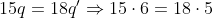
Portanto, o menor número multiplo de 15 e 18 ao mesmo tempo é 90(podemos usar o MMC também). Logo: n-12 = 90 ---> n=102