Arcos Duplos V
2 participantes
PiR2 :: Questões Especiais :: Olimpíadas :: Matemática
Página 1 de 1
Arcos Duplos V
por L.Lawliet Sáb 06 Set 2014, 21:52
Seja cos^6(3pi/8 - θ)+cos^6(pi/8-θ) ≡ m+n.sen(p.θ) com p > 0. Calcule (m+n+p)
Se tiver muito confuso, a expressão é: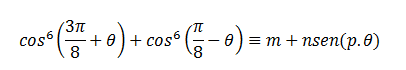
a)2
b)3
c)4
d)5
e)6
Se tiver muito confuso, a expressão é:
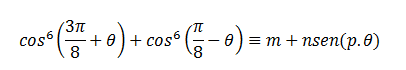
a)2
b)3
c)4
d)5
e)6
L.Lawliet- Mestre Jedi
- Mensagens : 797
Data de inscrição : 30/10/2013
Idade : 28
Localização : Brasil
Re: Arcos Duplos V
por Luck Dom 07 Set 2014, 18:43
Note que (3pi/8 + θ ) + (pi/8 - θ ) = pi/2 , assim, seja pi/8 - θ = x , temos:
(cosx)^6 + (senx)^6 ≡ m + nsen[((pi/8)-x)p]
S = (sen²x)³ + (cos²x)³
S = (sen²x + cos²x)((sen²x)² - sen²xcos²x + (cos²x)² )
S = 1( (sen²x+cos²x)² - 2sen²xcos²x - sen²xcos²x )
S = 1 - 3sen²xcos²x
1 - 3sen²xcos²x ≡ m + nsen[((pi/8)-x)p]
um valor viável é tomar p = 4, pois assim obtemos sen[(pi/2)-4x] = cos4x
1 - 3sen²xcos²x ≡ m + ncos4x
1 -3sen²xcos²x ≡ m + n ( 1 -2sen²(2x) )
1 - 3sen²xcos²x ≡ m + n ( 1 - 2(2senxcosx)² )
1- 3sen²cos²x ≡ m + n ( 1- 8sen²xcos²x)
1 - 3sen²xcos²x ≡ ( m + n) -8n(sen²xcos²x)
-3 = -8n ∴ n = 3/8
m+ n = 1 ∴ m = 5/8
m + n + p = 5
(cosx)^6 + (senx)^6 ≡ m + nsen[((pi/8)-x)p]
S = (sen²x)³ + (cos²x)³
S = (sen²x + cos²x)((sen²x)² - sen²xcos²x + (cos²x)² )
S = 1( (sen²x+cos²x)² - 2sen²xcos²x - sen²xcos²x )
S = 1 - 3sen²xcos²x
1 - 3sen²xcos²x ≡ m + nsen[((pi/8)-x)p]
um valor viável é tomar p = 4, pois assim obtemos sen[(pi/2)-4x] = cos4x
1 - 3sen²xcos²x ≡ m + ncos4x
1 -3sen²xcos²x ≡ m + n ( 1 -2sen²(2x) )
1 - 3sen²xcos²x ≡ m + n ( 1 - 2(2senxcosx)² )
1- 3sen²cos²x ≡ m + n ( 1- 8sen²xcos²x)
1 - 3sen²xcos²x ≡ ( m + n) -8n(sen²xcos²x)
-3 = -8n ∴ n = 3/8
m+ n = 1 ∴ m = 5/8
m + n + p = 5
Luck- Grupo
Velhos amigos do Fórum
- Mensagens : 5322
Data de inscrição : 20/09/2009
Idade : 32
Localização : RJ
Re: Arcos Duplos V
por L.Lawliet Dom 07 Set 2014, 19:30
Ah saquei. Valeu Luck!! Eu tava tentando gerar um seno linear no lado esquerdo. Teria como?
L.Lawliet- Mestre Jedi
- Mensagens : 797
Data de inscrição : 30/10/2013
Idade : 28
Localização : Brasil
Re: Arcos Duplos V
por Luck Dom 07 Set 2014, 22:41
No lado esquerdo vc também poderia ter desenvolvido em função do cosseno, trocando sen²x por 1 - cos²x , neste caso vc também desenvolveria o lado direito em função do cosseno cos4x = 2cos²(2x)-1, e analogamente cos2x = 2cos²x - 1 , chegaria ao mesmo resultado..luiz.bfg escreveu:Ah saquei. Valeu Luck!! Eu tava tentando gerar um seno linear no lado esquerdo. Teria como?
Luck- Grupo
Velhos amigos do Fórum - Mensagens : 5322
Data de inscrição : 20/09/2009
Idade : 32
Localização : RJ
L.Lawliet- Mestre Jedi
- Mensagens : 797
Data de inscrição : 30/10/2013
Idade : 28
Localização : Brasil
Tópicos semelhantesPiR2 :: Questões Especiais :: Olimpíadas :: Matemática
Página 1 de 1
Permissões neste sub-fórum
Não podes responder a tópicos
