Derivada segunda!!
2 participantes
Página 1 de 1
 Derivada segunda!!
Derivada segunda!!
Como obter a solução para:
(d^2(Ts)/dx^2
em 0<x<L
para Ts = T1 em x=0 e Ts=T2 em x=L
(d^2(Ts)/dx^2
em 0<x<L
para Ts = T1 em x=0 e Ts=T2 em x=L
PatGig- Iniciante
- Mensagens : 3
Data de inscrição : 24/05/2010
Idade : 34
Localização : sao paulo
 Re: Derivada segunda!!
Re: Derivada segunda!!
____________________________________________
In memoriam - Euclides faleceu na madrugada do dia 3 de Abril de 2018.

Lembre-se de que os vestibulares têm provas de Português também! Habitue-se a escrever corretamente em qualquer circunstância!
O Universo das coisas que eu não sei é incomensuravelmente maior do que o pacotinho de coisas que eu penso que sei.

Euclides- Fundador

- Mensagens : 32508
Data de inscrição : 07/07/2009
Idade : 74
Localização : São Paulo - SP
 Re: Derivada segunda!!
Re: Derivada segunda!!
A equação é essa mesmo, é parte da resolução de um problema de condução de calor em uma barra.
A resposta é Ts(x)=T1+(T2-T1).(x/L) mas não estou conseguindo chegar nessa solução!
A resposta é Ts(x)=T1+(T2-T1).(x/L) mas não estou conseguindo chegar nessa solução!
PatGig- Iniciante
- Mensagens : 3
Data de inscrição : 24/05/2010
Idade : 34
Localização : sao paulo
 Re: Derivada segunda!!
Re: Derivada segunda!!
O problema é o seguinte:
Uma barra, 00 a fronteira em x=0 e x=L é mantida a temperatura constante T1 e T2. Obtenha a expressão para a distribuição da temperatura T(x,t) na barra.

Uma barra, 0
PatGig- Iniciante
- Mensagens : 3
Data de inscrição : 24/05/2010
Idade : 34
Localização : sao paulo
 Re: Derivada segunda!!
Re: Derivada segunda!!
Ver a questão de exemplo - Clique Aqui
____________________________________________
In memoriam - Euclides faleceu na madrugada do dia 3 de Abril de 2018.

Lembre-se de que os vestibulares têm provas de Português também! Habitue-se a escrever corretamente em qualquer circunstância!
O Universo das coisas que eu não sei é incomensuravelmente maior do que o pacotinho de coisas que eu penso que sei.

Euclides- Fundador

- Mensagens : 32508
Data de inscrição : 07/07/2009
Idade : 74
Localização : São Paulo - SP
 Re: Derivada segunda!!
Re: Derivada segunda!!
A lei da condução térmica, também conhecida como lei de Fourier, estabelece que a taxa no tempo da transferência de calor através de um material é proporcional para o gradiente negativo na temperatura e na área em ângulos retos, para o gradiente, através do qual o calor está fluindo. Podemos afirmar, esta lei de duas formas equivalentes: a forma integral, em que olhamos para a quantidade de energia que flui para dentro ou para fora de um corpo como um todo, e na forma diferencial, em que olhamos para os fluxos de energia localmente.
Pode-se determinar o fluxo de calor transportado por condução pela Lei de Fourier:
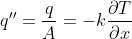
A expressão acima aplica-se ao caso unidimensional, quando há gradiente de temperatura apenas na direção x.
Caso se conheça as temperaturas de duas superfícies específicas e queira-se calcular o fluxo de calor por condução entre elas, basta integrar a equação acima, que toma a forma:
}{L})
A constante k, é a condutividade do material. Entre duas substâncias, a que tiver condutividade maior conseguirá transferir uma quantidade maior de calor, para uma mesma diferença de temperatura.
fonte: Wikipédia
Pode-se determinar o fluxo de calor transportado por condução pela Lei de Fourier:
A expressão acima aplica-se ao caso unidimensional, quando há gradiente de temperatura apenas na direção x.
Caso se conheça as temperaturas de duas superfícies específicas e queira-se calcular o fluxo de calor por condução entre elas, basta integrar a equação acima, que toma a forma:
A constante k, é a condutividade do material. Entre duas substâncias, a que tiver condutividade maior conseguirá transferir uma quantidade maior de calor, para uma mesma diferença de temperatura.
fonte: Wikipédia
____________________________________________
In memoriam - Euclides faleceu na madrugada do dia 3 de Abril de 2018.

Lembre-se de que os vestibulares têm provas de Português também! Habitue-se a escrever corretamente em qualquer circunstância!
O Universo das coisas que eu não sei é incomensuravelmente maior do que o pacotinho de coisas que eu penso que sei.

Euclides- Fundador

- Mensagens : 32508
Data de inscrição : 07/07/2009
Idade : 74
Localização : São Paulo - SP
Página 1 de 1
Permissões neste sub-fórum
Não podes responder a tópicos












