Perímetro
4 participantes
Página 1 de 1
Perímetro
por Man Utd Sex 19 Out 2012, 20:01
Um terreno de formato retangular deve ter perímetro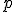 
. Determine as dimensões para as quais a área desse
terreno seja a maior possível.
terreno seja a maior possível.
Man Utd- Grupo
Velhos amigos do Fórum
- Mensagens : 1119
Data de inscrição : 18/08/2012
Idade : 30
Localização : Manchester
Re: Perímetro
por PedroX Sex 19 Out 2012, 20:16
A = a . b
Primeiramente notamos que as somas dos lados dão um número constante.
Sendo assim, para a área ser a maior possível, devemos ter medidas iguais.
Veja, por exemplo:
5² = 25
6.4 = 24
7.3 = 21
8.2 = 16
9.1 = 9
Ou seja, quanto mais próximos forem os valores, maior será o produto, levando em conta a constância das somas.
Como os lados são iguais, então cada um mede P/4.
Obs: o quadrado é um caso especial de retângulo.
Ate!
Primeiramente notamos que as somas dos lados dão um número constante.
Sendo assim, para a área ser a maior possível, devemos ter medidas iguais.
Veja, por exemplo:
5² = 25
6.4 = 24
7.3 = 21
8.2 = 16
9.1 = 9
Ou seja, quanto mais próximos forem os valores, maior será o produto, levando em conta a constância das somas.
Como os lados são iguais, então cada um mede P/4.
Obs: o quadrado é um caso especial de retângulo.
Ate!
PedroX- Administração
- Mensagens : 1041
Data de inscrição : 24/08/2011
Idade : 29
Localização : Campinas - SP
Man Utd- Grupo
Velhos amigos do Fórum - Mensagens : 1119
Data de inscrição : 18/08/2012
Idade : 30
Localização : Manchester
Re: Perímetro
por FernandoPP- Sáb 20 Out 2012, 18:46
Outra alternativa, Thiarlleson:
Chamando a e b os lados do retângulo, temos:
2a + 2b = P ⇒ a + b = P/2 ⇒ a = P/2 - b
Área do retângulo:
S = a.b ⇒ S = (P/2 - b).b
⇒ S = -b² + (P/2).b → A área do retângulo é expressa por um trinômio do 2º grau.
Como ele quer o valor dos LADOS para que a área seja a maior possível, então ele quer o X do vértice.
Xv = -b/2a ⇒ Xv = -(P/2)/2.(-1) ⇒ Xv = P/4 ⇒ b = P/4
Substituindo na equação anterior:
a = P/2 - P/4 ⇒ a = P/4
Como a = b, na verdade esta figura é um quadrado.
Chamando a e b os lados do retângulo, temos:
2a + 2b = P ⇒ a + b = P/2 ⇒ a = P/2 - b
Área do retângulo:
S = a.b ⇒ S = (P/2 - b).b
⇒ S = -b² + (P/2).b → A área do retângulo é expressa por um trinômio do 2º grau.
Como ele quer o valor dos LADOS para que a área seja a maior possível, então ele quer o X do vértice.
Xv = -b/2a ⇒ Xv = -(P/2)/2.(-1) ⇒ Xv = P/4 ⇒ b = P/4
Substituindo na equação anterior:
a = P/2 - P/4 ⇒ a = P/4
Como a = b, na verdade esta figura é um quadrado.
FernandoPP-- Jedi
- Mensagens : 354
Data de inscrição : 20/06/2012
Idade : 27
Localização : São Paulo, Brasil
raimundo pereira- Grupo
Velhos amigos do Fórum - Mensagens : 6114
Data de inscrição : 13/06/2012
Idade : 83
Localização : Rio de Janeiro
Página 1 de 1
Permissões neste sub-fórum
Não podes responder a tópicos
