Trapézio

por ricardo2012 Qui 21 Jun 2012, 22:56

Os ângulos da base maior de um trapézio são complementares, e a diferença entre suas medidas é 18º. O maior angulo desse trapézio mede

a) 100º
b) 126º
c) 144º
d) 152º

por **Elcioschin** Qui 21 Jun 2012, 23:07

a + b = 90º
a - b = 18º
----------------
2.a = 108º -----> a = 54º ----> b = 36º

y = 180º - a -----> y = 126º

x = 180º - b ----> x = 144º

por Mathematicien Sáb 02 Set 2017, 21:42

Elcioschin escreveu:a = b = 90º
a - b = 18º
----------------
2a = 108º -----> a = 54º ----> b = 3º

y = 180º - a -----> y = 126º

x = 180º - b ----> x = 144º

Mas Elcio, a soma desses ângulos dar 180° não é uma propriedade apenas dos trapézios isósceles? A questão não afirmou que é isósceles.

por **Elcioschin** Dom 03 Set 2017, 13:38

Não. A soma dos ângulos de cada lado inclinado do trapézio vale 180º para qualquer trapézio.

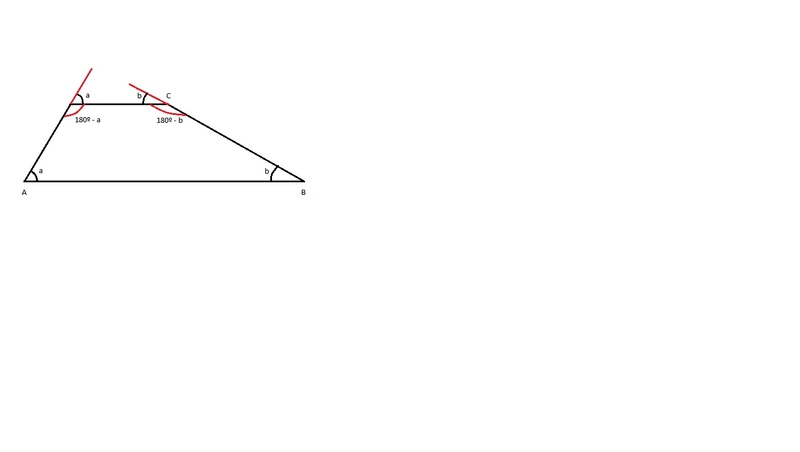
Desenhe o trapézio ABCD da questão, para confirmar:

AB = base maior, horizontal em baixo
CD = base menor, horizontal, em cima (AD e BC são os lados inclinados)

BÂD = a = 54º ---> A^BC = b = 36º (ângulos complementares)

y = A^DB = 180º - 54º ---> y = A^DB = 126º
x = B^CD = 180º - 36º ---> x = B^CD = 144º

Maior ângulo do trapézio = 144º

por Mathematicien Dom 03 Set 2017, 16:48

Essa propriedade é show de bola! Muito legal mesmo!

Consegui entender. Obrigado, Elcio!

por **Elcioschin** Dom 03 Set 2017, 18:29

E é uma propriedade facílima de demonstrar. Basta prolongar os lados AD e BC e usar a propriedade de duas paralelas (AB e CD) cortadas por uma transversal (AD ou BC), com ângulos alternos e externos.

por Mathematicien Seg 04 Set 2017, 11:52

Elcioschin escreveu:E é uma propriedade facílima de demonstrar. Basta prolongar os lados AD e BC e usar a propriedade de duas paralelas (AB e CD) cortadas por uma transversal (AD ou BC), com ângulos alternos e externos.