IME-2010
2 participantes
Página 1 de 1
IME-2010
por phBorges_32 Sex 22 Mar 2024, 16:35
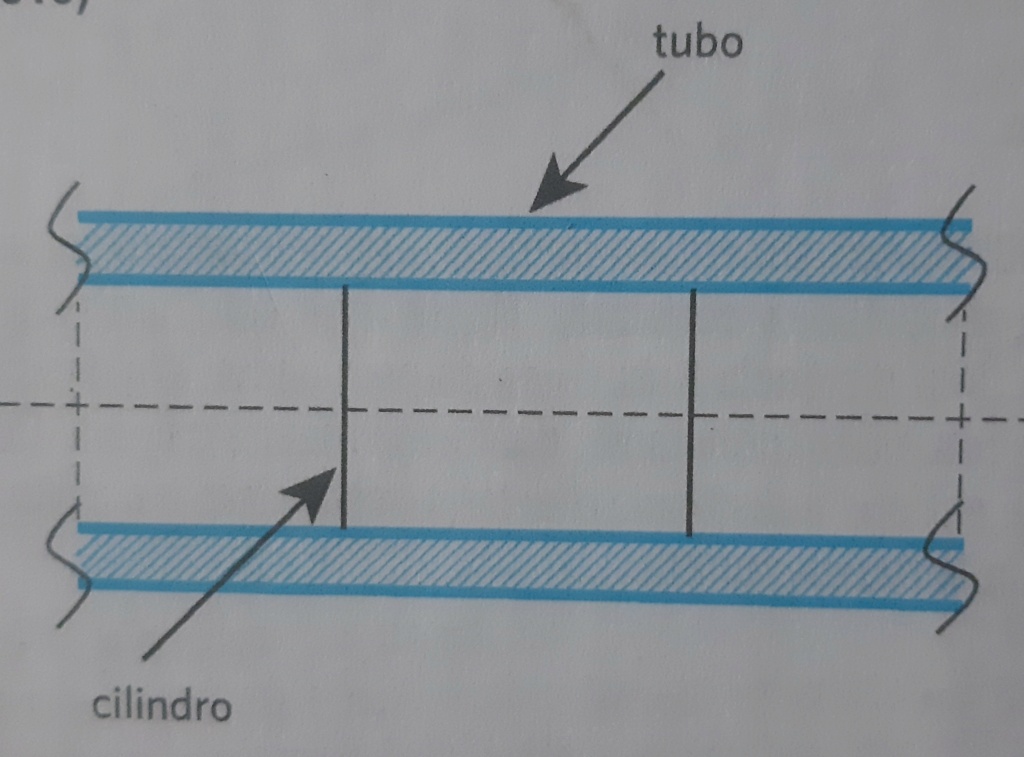
A figura acima apresenta um cilindro que executa um movimento simultâneo de translação e rotação com velocidades constantes no interior de um tubo longo. O cilindro está sempre coaxial ao tubo. A folga e o atrito entre o tubo e o cilindro são desprezíveis. Ao se deslocar no interior do tubo, o cilindro executa uma rotação completa em torno do seu eixo a cada 600 mm de comprimento do tubo. Sabendo que a velocidade de translação do cilindro é 6 m/s, a velocidade de rotação do cilindro em rpm é:
(A) 6.
(B) 10.
(C) 360.
(D) 600.
(E) 3.600.
phBorges_32- Iniciante
- Mensagens : 39
Data de inscrição : 24/02/2024
Idade : 20
Localização : Rio de janeiro
Giovana Martins gosta desta mensagem
phBorges_32- Iniciante
- Mensagens : 39
Data de inscrição : 24/02/2024
Idade : 20
Localização : Rio de janeiro
Giovana Martins gosta desta mensagem
Re: IME-2010
por Giovana Martins Sáb 23 Mar 2024, 15:49
A questão é um pouquinho complicada, porque há dois movimentos em execução.
Note que transladar, grosso modo, é o mesmo que andar para o lado (esquerdo ou direito, pois neste caso tanto faz).
Ao transladar 600 mm = 0,6 m o cilindro irá executar uma rotação. Para transladar 0,6 m, leva-se o seguinte tempo de execução, tendo em vista que a velocidade de translação corresponde a 6 m/s.
[latex]\\\mathrm{\Delta t_{Transladar}=\frac{\ell }{v}=\frac{0,6}{6}=0,1\ s}[/latex]
Como dito anteriormente, ao transladar 0,6 m (cujo tempo de execução corresponde a 0,1 s) o cilindro executará uma rotação. Assim, o cilindro leva 0,1 s para rotacionar, sendo 0,1 s o período de rotação do cilindro.
A frequência de rotação do cilindro é dada por:
[latex]\\\mathrm{f=\frac{1}{T}\to f=\frac{1}{0,1}\ \therefore\ f=10\ Hz=60\times 10=600\ rpm}[/latex]
[latex]\\\mathrm{\Delta t_{Transladar}=\frac{\ell }{v}=\frac{0,6}{6}=0,1\ s}[/latex]
Como dito anteriormente, ao transladar 0,6 m (cujo tempo de execução corresponde a 0,1 s) o cilindro executará uma rotação. Assim, o cilindro leva 0,1 s para rotacionar, sendo 0,1 s o período de rotação do cilindro.
A frequência de rotação do cilindro é dada por:
[latex]\\\mathrm{f=\frac{1}{T}\to f=\frac{1}{0,1}\ \therefore\ f=10\ Hz=60\times 10=600\ rpm}[/latex]
____________________________________________
Charlotte de Witte - Universal Nation
Giovana Martins- Grande Mestre
- Mensagens : 8563
Data de inscrição : 15/05/2015
Idade : 24
Localização : São Paulo
phBorges_32 gosta desta mensagem
phBorges_32- Iniciante
- Mensagens : 39
Data de inscrição : 24/02/2024
Idade : 20
Localização : Rio de janeiro
Giovana Martins gosta desta mensagem
Página 1 de 1
Permissões neste sub-fórum
Não podes responder a tópicos
