Stewart - Derivada Implícita

por Alberto Nascente Qui 15 Dez 2022, 08:07

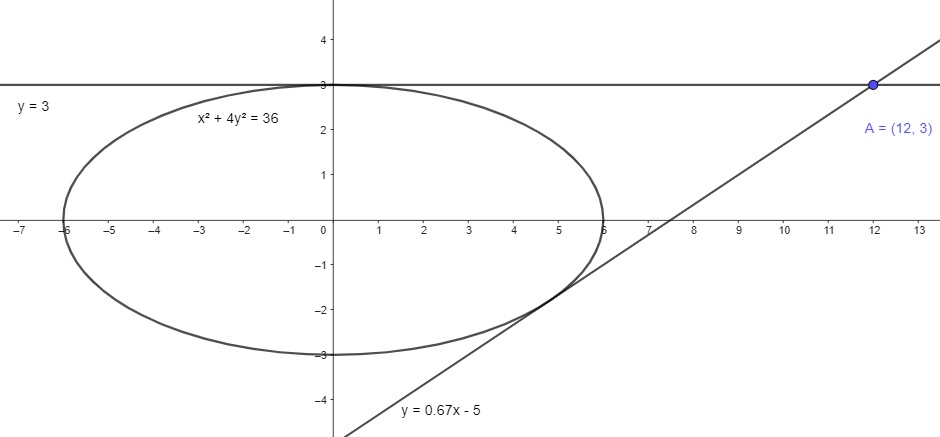
Encontre as equações de ambas as retas tangentes à elipse

Stewart - Derivada Implícita Svg+xml;base64,PD94bWwgdmVyc2lvbj0nMS4wJyBlbmNvZGluZz0nVVRGLTgnPz4KPCEtLSBHZW5lcmF0ZWQgYnkgQ29kZUNvZ3Mgd2l0aCBkdmlzdmdtIDIuMTMuMyAtLT4KPHN2ZyB2ZXJzaW9uPScxLjEnIHhtbG5zPSdodHRwOi8vd3d3LnczLm9yZy8yMDAwL3N2ZycgeG1sbnM6eGxpbms9J2h0dHA6Ly93d3cudzMub3JnLzE5OTkveGxpbmsnIHdpZHRoPSc3OC41MTE4OTVwdCcgaGVpZ2h0PScxNC4zMjI5MzZwdCcgdmlld0JveD0nLS4yMzkwNTEgLS4yMzUyNTQgNzguNTExODk1IDE0LjMyMjkzNic+CjxkZWZzPgo8cGF0aCBpZD0nZzItNDMnIGQ9J000Ljc3MDExMi0yLjc2MTY0NEg4LjA2OTczOEM4LjIzNzExMS0yLjc2MTY0NCA4LjQ1MjMwNC0yLjc2MTY0NCA4LjQ1MjMwNC0yLjk3NjgzN0M4LjQ1MjMwNC0zLjIwMzk4NSA4LjI0OTA2Ni0zLjIwMzk4NSA4LjA2OTczOC0zLjIwMzk4NUg0Ljc3MDExMlYtNi41MDM2MTFDNC43NzAxMTItNi42NzA5ODQgNC43NzAxMTItNi44ODYxNzcgNC41NTQ5MTktNi44ODYxNzdDNC4zMjc3NzEtNi44ODYxNzcgNC4zMjc3NzEtNi42ODI5MzkgNC4zMjc3NzEtNi41MDM2MTFWLTMuMjAzOTg1SDEuMDI4MTQ0Qy44NjA3NzItMy4yMDM5ODUgLjY0NTU3OS0zLjIwMzk4NSAuNjQ1NTc5LTIuOTg4NzkyQy42NDU1NzktMi43NjE2NDQgLjg0ODgxNy0yLjc2MTY0NCAxLjAyODE0NC0yLjc2MTY0NEg0LjMyNzc3MVYuNTM3OTgzQzQuMzI3NzcxIC43MDUzNTUgNC4zMjc3NzEgLjkyMDU0OCA0LjU0Mjk2NCAuOTIwNTQ4QzQuNzcwMTEyIC45MjA1NDggNC43NzAxMTIgLjcxNzMxIDQuNzcwMTEyIC41Mzc5ODNWLTIuNzYxNjQ0WicvPgo8cGF0aCBpZD0nZzItNTEnIGQ9J00yLjE5OTc1MS00LjI5MTkwNUMxLjk5NjUxMy00LjI3OTk1IDEuOTQ4NjkyLTQuMjY3OTk1IDEuOTQ4NjkyLTQuMTYwMzk5QzEuOTQ4NjkyLTQuMDQwODQ3IDIuMDA4NDY4LTQuMDQwODQ3IDIuMjIzNjYxLTQuMDQwODQ3SDIuNzczNTk5QzMuNzg5Nzg4LTQuMDQwODQ3IDQuMjQ0MDg1LTMuMjAzOTg1IDQuMjQ0MDg1LTIuMDU2Mjg5QzQuMjQ0MDg1LS40OTAxNjIgMy40MzExMzMtLjA3MTczMSAyLjg0NTMzLS4wNzE3MzFDMi4yNzE0ODItLjA3MTczMSAxLjI5MTE1OC0uMzQ2NyAuOTQ0NDU4LTEuMTM1NzQxQzEuMzI3MDI0LTEuMDc1OTY1IDEuNjczNzI0LTEuMjkxMTU4IDEuNjczNzI0LTEuNzIxNTQ0QzEuNjczNzI0LTIuMDY4MjQ0IDEuNDIyNjY1LTIuMzA3MzQ3IDEuMDg3OTItMi4zMDczNDdDLjgwMDk5Ni0yLjMwNzM0NyAuNDkwMTYyLTIuMTM5OTc1IC40OTAxNjItMS42ODU2NzlDLjQ5MDE2Mi0uNjIxNjY5IDEuNTU0MTcyIC4yNTEwNTkgMi44ODExOTYgLjI1MTA1OUM0LjMwMzg2MSAuMjUxMDU5IDUuMzU1OTE1LS44MzY4NjIgNS4zNTU5MTUtMi4wNDQzMzRDNS4zNTU5MTUtMy4xNDQyMDkgNC40NzEyMzMtNC4wMDQ5ODEgMy4zMjM1MzctNC4yMDgyMTlDNC4zNjM2MzYtNC41MDcwOTggNS4wMzMxMjYtNS4zNzk4MjYgNS4wMzMxMjYtNi4zMTIzMjlDNS4wMzMxMjYtNy4yNTY3ODcgNC4wNTI4MDItNy45NTAxODcgMi44OTMxNTEtNy45NTAxODdDMS42OTc2MzQtNy45NTAxODcgLjgxMjk1MS03LjIyMDkyMiAuODEyOTUxLTYuMzQ4MTk0Qy44MTI5NTEtNS44Njk5ODggMS4xODM1NjItNS43NzQzNDYgMS4zNjI4ODktNS43NzQzNDZDMS42MTM5NDgtNS43NzQzNDYgMS45MDA4NzItNS45NTM2NzQgMS45MDA4NzItNi4zMTIzMjlDMS45MDA4NzItNi42OTQ4OTQgMS42MTM5NDgtNi44NjIyNjcgMS4zNTA5MzQtNi44NjIyNjdDMS4yNzkyMDMtNi44NjIyNjcgMS4yNTUyOTMtNi44NjIyNjcgMS4yMTk0MjctNi44NTAzMTFDMS42NzM3MjQtNy42NjMyNjMgMi43OTc1MDktNy42NjMyNjMgMi44NTcyODUtNy42NjMyNjNDMy4yNTE4MDYtNy42NjMyNjMgNC4wMjg4OTItNy40ODM5MzUgNC4wMjg4OTItNi4zMTIzMjlDNC4wMjg4OTItNi4wODUxODEgMy45OTMwMjYtNS40MTU2OTEgMy42NDYzMjYtNC45MDE2MTlDMy4yODc2NzEtNC4zNzU1OTIgMi44ODExOTYtNC4zMzk3MjYgMi41NTg0MDYtNC4zMjc3NzFMMi4xOTk3NTEtNC4yOTE5MDVaJy8+CjxwYXRoIGlkPSdnMi01MicgZD0nTTQuMzE1ODE2LTcuNzgyODE0QzQuMzE1ODE2LTguMDA5OTYzIDQuMzE1ODE2LTguMDY5NzM4IDQuMTQ4NDQzLTguMDY5NzM4QzQuMDUyODAyLTguMDY5NzM4IDQuMDE2OTM2LTguMDY5NzM4IDMuOTIxMjk1LTcuOTI2Mjc2TC4zMjI3OS0yLjM0MzIxM1YtMS45OTY1MTNIMy40NjY5OTlWLS45MDg1OTNDMy40NjY5OTktLjQ2NjI1MiAzLjQ0MzA4OC0uMzQ2NyAyLjU3MDM2MS0uMzQ2N0gyLjMzMTI1OFYwQzIuNjA2MjI3LS4wMjM5MSAzLjU1MDY4NS0uMDIzOTEgMy44ODU0My0uMDIzOTFTNS4xNzY1ODgtLjAyMzkxIDUuNDUxNTU3IDBWLS4zNDY3SDUuMjEyNDUzQzQuMzUxNjgxLS4zNDY3IDQuMzE1ODE2LS40NjYyNTIgNC4zMTU4MTYtLjkwODU5M1YtMS45OTY1MTNINS41MjMyODhWLTIuMzQzMjEzSDQuMzE1ODE2Vi03Ljc4MjgxNFpNMy41MjY3NzUtNi44NTAzMTFWLTIuMzQzMjEzSC42MjE2NjlMMy41MjY3NzUtNi44NTAzMTFaJy8+CjxwYXRoIGlkPSdnMi01NCcgZD0nTTEuNDcwNDg2LTQuMTYwMzk5QzEuNDcwNDg2LTcuMTg1MDU2IDIuOTQwOTcxLTcuNjYzMjYzIDMuNTg2NTUtNy42NjMyNjNDNC4wMTY5MzYtNy42NjMyNjMgNC40NDczMjMtNy41MzE3NTYgNC42NzQ0NzEtNy4xNzMxMDFDNC41MzEwMDktNy4xNzMxMDEgNC4wNzY3MTItNy4xNzMxMDEgNC4wNzY3MTItNi42ODI5MzlDNC4wNzY3MTItNi40MTk5MjUgNC4yNTYwNC02LjE5Mjc3NyA0LjU2Njg3NC02LjE5Mjc3N0M0Ljg2NTc1My02LjE5Mjc3NyA1LjA2ODk5MS02LjM3MjEwNSA1LjA2ODk5MS02LjcxODgwNEM1LjA2ODk5MS03LjM0MDQ3MyA0LjYxNDY5NS03Ljk1MDE4NyAzLjU3NDU5NS03Ljk1MDE4N0MyLjA2ODI0NC03Ljk1MDE4NyAuNDkwMTYyLTYuNDA3OTcgLjQ5MDE2Mi0zLjc3NzgzM0MuNDkwMTYyLS40OTAxNjIgMS45MjQ3ODIgLjI1MTA1OSAyLjk0MDk3MSAuMjUxMDU5QzQuMjQ0MDg1IC4yNTEwNTkgNS4zNTU5MTUtLjg4NDY4MiA1LjM1NTkxNS0yLjQzODg1NEM1LjM1NTkxNS00LjAyODg5MiA0LjI0NDA4NS01LjA5MjkwMiAzLjA0ODU2OC01LjA5MjkwMkMxLjk4NDU1OC01LjA5MjkwMiAxLjU5MDAzNy00LjE3MjM1NCAxLjQ3MDQ4Ni0zLjgzNzYwOVYtNC4xNjAzOTlaTTIuOTQwOTcxLS4wNzE3MzFDMi4xODc3OTYtLjA3MTczMSAxLjgyOTE0MS0uNzQxMjIgMS43MjE1NDQtLjk5MjI3OUMxLjYxMzk0OC0xLjMwMzExMyAxLjQ5NDM5Ni0xLjg4ODkxNyAxLjQ5NDM5Ni0yLjcyNTc3OEMxLjQ5NDM5Ni0zLjY3MDIzNyAxLjkyNDc4Mi00Ljg1Mzc5OCAzLjAwMDc0Ny00Ljg1Mzc5OEMzLjY1ODI4MS00Ljg1Mzc5OCA0LjAwNDk4MS00LjQxMTQ1NyA0LjE4NDMwOS00LjAwNDk4MUM0LjM3NTU5Mi0zLjU2MjY0IDQuMzc1NTkyLTIuOTY0ODgyIDQuMzc1NTkyLTIuNDUwODA5QzQuMzc1NTkyLTEuODQxMDk2IDQuMzc1NTkyLTEuMzAzMTEzIDQuMTQ4NDQzLS44NDg4MTdDMy44NDk1NjQtLjI3NDk2OSAzLjQxOTE3OC0uMDcxNzMxIDIuOTQwOTcxLS4wNzE3MzFaJy8+CjxwYXRoIGlkPSdnMi02MScgZD0nTTguMDY5NzM4LTMuODczNDc0QzguMjM3MTExLTMuODczNDc0IDguNDUyMzA0LTMuODczNDc0IDguNDUyMzA0LTQuMDg4NjY3QzguNDUyMzA0LTQuMzE1ODE2IDguMjQ5MDY2LTQuMzE1ODE2IDguMDY5NzM4LTQuMzE1ODE2SDEuMDI4MTQ0Qy44NjA3NzItNC4zMTU4MTYgLjY0NTU3OS00LjMxNTgxNiAuNjQ1NTc5LTQuMTAwNjIzQy42NDU1NzktMy44NzM0NzQgLjg0ODgxNy0zLjg3MzQ3NCAxLjAyODE0NC0zLjg3MzQ3NEg4LjA2OTczOFpNOC4wNjk3MzgtMS42NDk4MTNDOC4yMzcxMTEtMS42NDk4MTMgOC40NTIzMDQtMS42NDk4MTMgOC40NTIzMDQtMS44NjUwMDZDOC40NTIzMDQtMi4wOTIxNTQgOC4yNDkwNjYtMi4wOTIxNTQgOC4wNjk3MzgtMi4wOTIxNTRIMS4wMjgxNDRDLjg2MDc3Mi0yLjA5MjE1NCAuNjQ1NTc5LTIuMDkyMTU0IC42NDU1NzktMS44NzY5NjFDLjY0NTU3OS0xLjY0OTgxMyAuODQ4ODE3LTEuNjQ5ODEzIDEuMDI4MTQ0LTEuNjQ5ODEzSDguMDY5NzM4WicvPgo8cGF0aCBpZD0nZzEtNTAnIGQ9J00yLjI0NzU3Mi0xLjYyNTkwM0MyLjM3NTA5My0xLjc0NTQ1NSAyLjcwOTgzOC0yLjAwODQ2OCAyLjgzNzM2LTIuMTIwMDVDMy4zMzE1MDctMi41NzQzNDYgMy44MDE3NDMtMy4wMTI3MDIgMy44MDE3NDMtMy43Mzc5ODNDMy44MDE3NDMtNC42ODY0MjYgMy4wMDQ3MzItNS4zMDAxMjUgMi4wMDg0NjgtNS4zMDAxMjVDMS4wNTIwNTUtNS4zMDAxMjUgLjQyMjQxNi00LjU3NDg0NCAuNDIyNDE2LTMuODY1NTA0Qy40MjI0MTYtMy40NzQ5NjkgLjczMzI1LTMuNDE5MTc4IC44NDQ4MzItMy40MTkxNzhDMS4wMTIyMDQtMy40MTkxNzggMS4yNTkyNzgtMy41Mzg3MyAxLjI1OTI3OC0zLjg0MTU5NEMxLjI1OTI3OC00LjI1NjA0IC44NjA3NzItNC4yNTYwNCAuNzY1MTMxLTQuMjU2MDRDLjk5NjI2NC00LjgzNzg1OCAxLjUzMDI2Mi01LjAzNzExMSAxLjkyMDc5Ny01LjAzNzExMUMyLjY2MjAxNy01LjAzNzExMSAzLjA0NDU4My00LjQwNzQ3MiAzLjA0NDU4My0zLjczNzk4M0MzLjA0NDU4My0yLjkwOTA5MSAyLjQ2Mjc2NS0yLjMwMzM2MiAxLjUyMjI5MS0xLjMzODk3OUwuNTE4MDU3LS4zMDI4NjRDLjQyMjQxNi0uMjE1MTkzIC40MjI0MTYtLjE5OTI1MyAuNDIyNDE2IDBIMy41NzA2MUwzLjgwMTc0My0xLjQyNjY1SDMuNTU0NjdDMy41MzA3Ni0xLjI2NzI0OCAzLjQ2Njk5OS0uODY4NzQyIDMuMzcxMzU3LS43MTczMUMzLjMyMzUzNy0uNjUzNTQ5IDIuNzE3ODA4LS42NTM1NDkgMi41OTAyODYtLjY1MzU0OUgxLjE3MTYwNkwyLjI0NzU3Mi0xLjYyNTkwM1onLz4KPHBhdGggaWQ9J2cwLTEyMCcgZD0nTTUuNjY2NzUtNC44Nzc3MDlDNS4yODQxODQtNC44MDU5NzggNS4xNDA3MjItNC41MTkwNTQgNS4xNDA3MjItNC4yOTE5MDVDNS4xNDA3MjItNC4wMDQ5ODEgNS4zNjc4Ny0zLjkwOTM0IDUuNTM1MjQzLTMuOTA5MzRDNS44OTM4OTgtMy45MDkzNCA2LjE0NDk1Ni00LjIyMDE3NCA2LjE0NDk1Ni00LjU0Mjk2NEM2LjE0NDk1Ni01LjA0NTA4MSA1LjU3MTEwOC01LjI3MjIyOSA1LjA2ODk5MS01LjI3MjIyOUM0LjMzOTcyNi01LjI3MjIyOSAzLjkzMzI1LTQuNTU0OTE5IDMuODI1NjU0LTQuMzI3NzcxQzMuNTUwNjg1LTUuMjI0NDA4IDIuODA5NDY1LTUuMjcyMjI5IDIuNTk0MjcxLTUuMjcyMjI5QzEuMzc0ODQ0LTUuMjcyMjI5IC43MjkyNjUtMy43MDYxMDIgLjcyOTI2NS0zLjQ0MzA4OEMuNzI5MjY1LTMuMzk1MjY4IC43NzcwODYtMy4zMzU0OTIgLjg2MDc3Mi0zLjMzNTQ5MkMuOTU2NDEzLTMuMzM1NDkyIC45ODAzMjQtMy40MDcyMjMgMS4wMDQyMzQtMy40NTUwNDRDMS40MTA3MS00Ljc4MjA2NyAyLjIxMTcwNi01LjAzMzEyNiAyLjU1ODQwNi01LjAzMzEyNkMzLjA5NjM4OS01LjAzMzEyNiAzLjIwMzk4NS00LjUzMTAwOSAzLjIwMzk4NS00LjI0NDA4NUMzLjIwMzk4NS0zLjk4MTA3MSAzLjEzMjI1NC0zLjcwNjEwMiAyLjk4ODc5Mi0zLjEzMjI1NEwyLjU4MjMxNi0xLjQ5NDM5NkMyLjQwMjk4OS0uNzc3MDg2IDIuMDU2Mjg5LS4xMTk1NTIgMS40MjI2NjUtLjExOTU1MkMxLjM2Mjg4OS0uMTE5NTUyIDEuMDY0MDEtLjExOTU1MiAuODEyOTUxLS4yNzQ5NjlDMS4yNDMzMzctLjM1ODY1NSAxLjMzODk3OS0uNzE3MzEgMS4zMzg5NzktLjg2MDc3MkMxLjMzODk3OS0xLjA5OTg3NSAxLjE1OTY1MS0xLjI0MzMzNyAuOTMyNTAzLTEuMjQzMzM3Qy42NDU1NzktMS4yNDMzMzcgLjMzNDc0NS0uOTkyMjc5IC4zMzQ3NDUtLjYwOTcxNEMuMzM0NzQ1LS4xMDc1OTcgLjg5NjYzOCAuMTE5NTUyIDEuNDEwNzEgLjExOTU1MkMxLjk4NDU1OCAuMTE5NTUyIDIuMzkxMDM0LS4zMzQ3NDUgMi42NDIwOTItLjgyNDkwN0MyLjgzMzM3NS0uMTE5NTUyIDMuNDMxMTMzIC4xMTk1NTIgMy44NzM0NzQgLjExOTU1MkM1LjA5MjkwMiAuMTE5NTUyIDUuNzM4NDgxLTEuNDQ2NTc1IDUuNzM4NDgxLTEuNzA5NTg5QzUuNzM4NDgxLTEuNzY5MzY1IDUuNjkwNjYtMS44MTcxODYgNS42MTg5MjktMS44MTcxODZDNS41MTEzMzMtMS44MTcxODYgNS40OTkzNzctMS43NTc0MSA1LjQ2MzUxMi0xLjY2MTc2OEM1LjE0MDcyMi0uNjA5NzE0IDQuNDQ3MzIzLS4xMTk1NTIgMy45MDkzNC0uMTE5NTUyQzMuNDkwOTA5LS4xMTk1NTIgMy4yNjM3NjEtLjQzMDM4NiAzLjI2Mzc2MS0uOTIwNTQ4QzMuMjYzNzYxLTEuMTgzNTYyIDMuMzExNTgyLTEuMzc0ODQ0IDMuNTAyODY0LTIuMTYzODg1TDMuOTIxMjk1LTMuNzg5Nzg4QzQuMTAwNjIzLTQuNTA3MDk4IDQuNTA3MDk4LTUuMDMzMTI2IDUuMDU3MDM2LTUuMDMzMTI2QzUuMDgwOTQ2LTUuMDMzMTI2IDUuNDE1NjkxLTUuMDMzMTI2IDUuNjY2NzUtNC44Nzc3MDlaJy8+CjxwYXRoIGlkPSdnMC0xMjEnIGQ9J00zLjE0NDIwOSAxLjMzODk3OUMyLjgyMTQyIDEuNzkzMjc1IDIuMzU1MTY4IDIuMTk5NzUxIDEuNzY5MzY1IDIuMTk5NzUxQzEuNjI1OTAzIDIuMTk5NzUxIDEuMDUyMDU1IDIuMTc1ODQxIC44NzI3MjcgMS42MjU5MDNDLjkwODU5MyAxLjYzNzg1OCAuOTY4MzY5IDEuNjM3ODU4IC45OTIyNzkgMS42Mzc4NThDMS4zNTA5MzQgMS42Mzc4NTggMS41OTAwMzcgMS4zMjcwMjQgMS41OTAwMzcgMS4wNTIwNTVTMS4zNjI4ODkgLjY4MTQ0NSAxLjE4MzU2MiAuNjgxNDQ1Qy45OTIyNzkgLjY4MTQ0NSAuNTczODQ4IC44MjQ5MDcgLjU3Mzg0OCAxLjQxMDcxQy41NzM4NDggMi4wMjA0MjMgMS4wODc5MiAyLjQzODg1NCAxLjc2OTM2NSAyLjQzODg1NEMyLjk2NDg4MiAyLjQzODg1NCA0LjE3MjM1NCAxLjMzODk3OSA0LjUwNzA5OCAuMDExOTU1TDUuNjc4NzA1LTQuNjUwNTZDNS42OTA2Ni00LjcxMDMzNiA1LjcxNDU3LTQuNzgyMDY3IDUuNzE0NTctNC44NTM3OThDNS43MTQ1Ny01LjAzMzEyNiA1LjU3MTEwOC01LjE1MjY3NyA1LjM5MTc4MS01LjE1MjY3N0M1LjI4NDE4NC01LjE1MjY3NyA1LjAzMzEyNi01LjEwNDg1NyA0LjkzNzQ4NC00Ljc0NjIwMkw0LjA1MjgwMi0xLjIzMTM4MkMzLjk5MzAyNi0xLjAxNjE4OSAzLjk5MzAyNi0uOTkyMjc5IDMuODk3Mzg1LS44NjA3NzJDMy42NTgyODEtLjUyNjAyNyAzLjI2Mzc2MS0uMTE5NTUyIDIuNjg5OTEzLS4xMTk1NTJDMi4wMjA0MjMtLjExOTU1MiAxLjk2MDY0OC0uNzc3MDg2IDEuOTYwNjQ4LTEuMDk5ODc1QzEuOTYwNjQ4LTEuNzgxMzIgMi4yODM0MzctMi43MDE4NjggMi42MDYyMjctMy41NjI2NEMyLjczNzczMy0zLjkwOTM0IDIuODA5NDY1LTQuMDc2NzEyIDIuODA5NDY1LTQuMzE1ODE2QzIuODA5NDY1LTQuODE3OTMzIDIuNDUwODA5LTUuMjcyMjI5IDEuODY1MDA2LTUuMjcyMjI5Qy43NjUxMzEtNS4yNzIyMjkgLjMyMjc5LTMuNTM4NzMgLjMyMjc5LTMuNDQzMDg4Qy4zMjI3OS0zLjM5NTI2OCAuMzcwNjEtMy4zMzU0OTIgLjQ1NDI5Ni0zLjMzNTQ5MkMuNTYxODkzLTMuMzM1NDkyIC41NzM4NDgtMy4zODMzMTMgLjYyMTY2OS0zLjU1MDY4NUMuOTA4NTkzLTQuNTU0OTE5IDEuMzYyODg5LTUuMDMzMTI2IDEuODI5MTQxLTUuMDMzMTI2QzEuOTM2NzM3LTUuMDMzMTI2IDIuMTM5OTc1LTUuMDMzMTI2IDIuMTM5OTc1LTQuNjM4NjA1QzIuMTM5OTc1LTQuMzI3NzcxIDIuMDA4NDY4LTMuOTgxMDcxIDEuODI5MTQxLTMuNTI2Nzc1QzEuMjQzMzM3LTEuOTYwNjQ4IDEuMjQzMzM3LTEuNTY2MTI3IDEuMjQzMzM3LTEuMjc5MjAzQzEuMjQzMzM3LS4xNDM0NjIgMi4wNTYyODkgLjExOTU1MiAyLjY1NDA0NyAuMTE5NTUyQzMuMDAwNzQ3IC4xMTk1NTIgMy40MzExMzMgLjAxMTk1NSAzLjg0OTU2NC0uNDMwMzg2TDMuODYxNTE5LS40MTg0MzFDMy42ODIxOTIgLjI4NjkyNCAzLjU2MjY0IC43NTMxNzYgMy4xNDQyMDkgMS4zMzg5NzlaJy8+CjwvZGVmcz4KPGcgaWQ9J3BhZ2UxJyB0cmFuc2Zvcm09J21hdHJpeCgxLjEzIDAgMCAxLjEzIC02My45ODYwNDMgLTYyLjk2OTU5MyknPgo8dXNlIHg9JzU2LjQxMzI2NycgeT0nNjUuNzUzNDI1JyB4bGluazpocmVmPScjZzAtMTIwJy8+Cjx1c2UgeD0nNjMuMDY1MzU0JyB5PSc2MC44MTcyMzknIHhsaW5rOmhyZWY9JyNnMS01MCcvPgo8dXNlIHg9JzcwLjQ1NDMzMycgeT0nNjUuNzUzNDI1JyB4bGluazpocmVmPScjZzItNDMnLz4KPHVzZSB4PSc4Mi4yMTU2NDgnIHk9JzY1Ljc1MzQyNScgeGxpbms6aHJlZj0nI2cyLTUyJy8+Cjx1c2UgeD0nODguMDY4NjM4JyB5PSc2NS43NTM0MjUnIHhsaW5rOmhyZWY9JyNnMC0xMjEnLz4KPHVzZSB4PSc5NC4yMDUyOScgeT0nNjAuODE3MjM5JyB4bGluazpocmVmPScjZzEtNTAnLz4KPHVzZSB4PScxMDIuMjU4NDM0JyB5PSc2NS43NTM0MjUnIHhsaW5rOmhyZWY9JyNnMi02MScvPgo8dXNlIHg9JzExNC42ODM5MTUnIHk9JzY1Ljc1MzQyNScgeGxpbms6aHJlZj0nI2cyLTUxJy8+Cjx1c2UgeD0nMTIwLjUzNjkwNScgeT0nNjUuNzUzNDI1JyB4bGluazpocmVmPScjZzItNTQnLz4KPC9nPgo8L3N2Zz4=

que passam pelo ponto (12,3)
S/ gabarito.

Derivei implicitamente, como em tese o capítulo ensina a fazer.
Porém, a reta que eu achei n eh tangente a curva, ela apenas passa pelo ponto dado...
Como pode resolver isso?

Obrigado! Very Happy

por **Elcioschin** Qui 15 Dez 2022, 11:10

Sem derivar

Equação geral das retas ---> y - 3 = m.(x - 12) ---> y = m.x + 3 - 12.m

Substitua na equação da elipse e chegue numa equação do 2º grau em x

Paras as retas serem tangentes o discriminante ∆ deverá ser nulo ---> ∆ = 0 ---> Calcule m

por Alberto Nascente Qui 15 Dez 2022, 14:29

Ah sim, eu havia feito sem derivar tbm.
A questão eh q o exercício pede para ser feito usando derivada implícita, aí só consigo resolver se for pela geo. analítica.

O senhor sabe como q eu posso fazer esses cálculos derivando implicitamente?

Obrigado! Very Happy

por **tales amaral** Qui 15 Dez 2022, 14:41

Pra mim deu a mesma coisa. O ponto não tá na curva kk.

por Alberto Nascente Sex 16 Dez 2022, 08:30

Sim, vdd Tales
Quando derivei implicitamente, achei uma reta passando por um ponto dado q n está na curva, e essa reta nem passava pela curva tbm.

Seria um erro nosso? Ou de digitação da questão?

por **petras** Sex 16 Dez 2022, 09:18

Alberto Nascente escreveu:Encontre as equações de ambas as retas tangentes à elipse que passam pelo ponto (12,3)
S/ gabarito.

Derivei implicitamente, como em tese o capítulo ensina a fazer.
Porém, a reta que eu achei n eh tangente a curva, ela apenas passa pelo ponto dado...
Como pode resolver isso?

Obrigado!

[latex]\\x^2+4y^2 = 36(I) \implies 2xdx + 8ydy = 0 \implies \frac{dx}{dy} = -\frac{x}{4y} 4y^2 = 36-x^2(II)\\ r:y - y_o = \frac{dy}{dx}(x-x_o)\\ (12,3) \in r: y-3= -\frac{x}{4y}(x-12)\implies 4y^2-12y=-x^2+12x\\ De(II): (36-x^2)-12y=-x^2+12x \therefore y = -x+3\\ Substituindo(I): x^2+4(-x+3)^2=36\implies x(x-\frac{24}{5})=0\\ \therefore x = 0\implies y = -0+3=3\\ ~ou~x = \frac{24}{5}\implies y = -\frac{24}{5}+3 = -\frac{9}{5}\\ \frac{dy}{dx} = -\frac{x}{4y} = -\frac{0}{3} = 0\\ y -y_o = \frac{dy}{dx}(x-x_o)\implies y-3 = 0(x-0) = 3 \therefore \boxed{y=3}\\ (\frac{24}{5}, -\frac{9}{5}): y + \frac{9}{5}=\frac{2}{3}(x-\frac{24}{5} \implies \boxed{y=\frac{2x}{3}-5} [/latex]

(Solução:nakagumahissao)