Quadriláteros
2 participantes
Página 1 de 1
Quadriláteros
por Lucas Garibaldi Seg 20 Jun 2022, 00:45
Uma reta r divide um retângulo ABCD em dois trapézios, de tal forma que a área do trapézio ADPQ é a quarta parte da área desse retângulo.
Sabendo que DP = 1,4 cm e AQ = 3,2 cm.
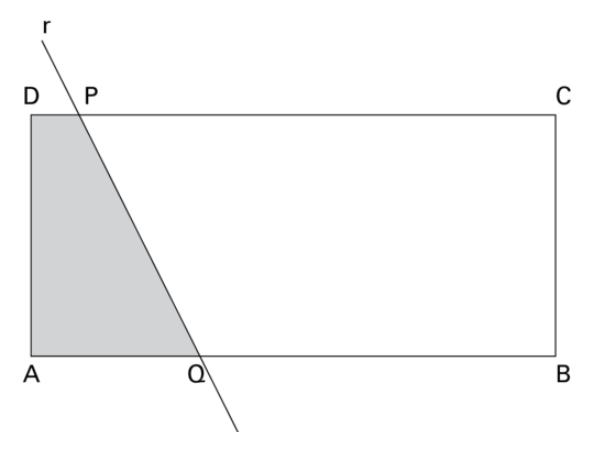
A diferença entre as medianas de Euler dos trapézios BCPQ e ADPQ, em cm, é
Sabendo que DP = 1,4 cm e AQ = 3,2 cm.
A diferença entre as medianas de Euler dos trapézios BCPQ e ADPQ, em cm, é
A0.
B0,9.
C
1,8.
D
2,7.
E
3,2.
Lucas Garibaldi- Recebeu o sabre de luz
- Mensagens : 132
Data de inscrição : 27/06/2021
Re: Quadriláteros
por petras Seg 20 Jun 2022, 09:34
[latex]M_e(AQPD)=\frac{3,2-1,4}{2}=0,9(I)\\ M(AQPD)=\frac{3,2+1,4}{2} = 2,3\\ S_{AQPD} =2,3 . h = \frac{S_{ABCD}}{4}=AB.h \therefore AB =9,2 \\ BQ = 9,2-AQ =9,2-3.2=6\\ CP = 9,2 - 1,4 = 7,8\\ \therefore M_e(BCPQ) = \frac{7,8-6}{2}=0,9(II)\\ (I)-(II) = 0[/latex]
____________________________________________
_______________________________
"Ex nihilo nihil fit"
petras- Monitor
- Mensagens : 2117
Data de inscrição : 10/06/2016
Idade : 59
Localização : bragança, sp, brasil
Página 1 de 1
Permissões neste sub-fórum
Não podes responder a tópicos
