Geometria Espacial

por mv.valiati Qui 26 maio 2022, 13:25

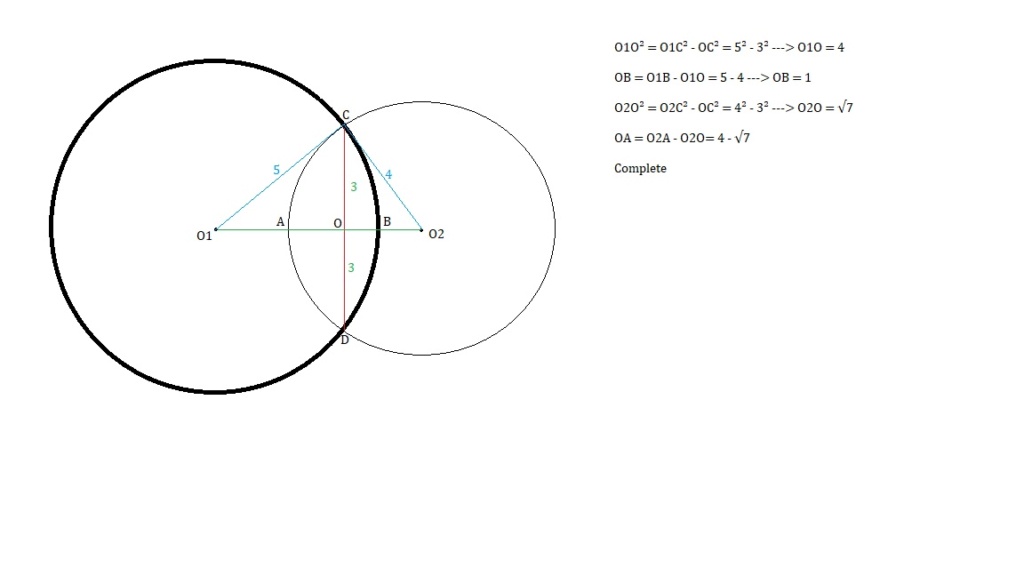
Se duas esferas de raios 5cm e 4cm centros, respectivamente O1 e O2, se intersectam em uma circunferência de raio 3cm, então a distância entre os centros O1 e O2 é

_______ ou ___________. (representação decimal com duas casas decimais em ordem crescente).

por **Elcioschin** Qui 26 maio 2022, 16:43

por mv.valiati Sex 27 maio 2022, 14:26

Elcioschin escreveu:

por mv.valiati Sex 27 maio 2022, 20:59

Elcioschin escreveu:

Fiquei com dúvida sobre o que o enunciado pede. Eu entendi que ele quer a distância de entre o1 e o2. Seria isso ?
Ou ele pede as distâncias de o1 a 0 e o2 a 0?

por **Elcioschin** Sex 27 maio 2022, 21:50

O enunciado é bem claro: "..... a distância entre os centros O1 e O2" é

O1O + O2O = O1O2

por mv.valiati Sex 27 maio 2022, 21:57

Foi o que eu entendi, eu fiquei com essa dúvida porque o problema tem espaço pra duas resposta. E a distância o1o2 é única. Certo ?

por **Elcioschin** Sex 27 maio 2022, 22:10

Uma resposta no formato irracional e outra em formato decimal

por Silvano marinho Sáb 28 maio 2022, 07:56

Em um poliedro P não necessariamente convexo, com V vértices, A arestas e F faces, a característica de Euler desse poliedro é o número X(P) = V - A + F.
A partir de um poliedro P com todas as faces convexas pode-se formar um novo poliedro P' apenas com faces triangulares escolhendo-se um vértice em cada face e traçando-se todas as diagonais dessa face que partem do vértice escolhido.
Assim, essas diagonais passam a ser arestas do poliedro P' e os triângulos formados passam a serem faces de P'.
O valor de |X(P') - X(P)| = Resposta (número inteiro em representação simbólica. Não escreva por extenso).

por **Elcioschin** Sáb 28 maio 2022, 09:18

Silvano marinho

As Regras do fórum não permitem "pegar carona" numa questão existente para postar outras questões.
Você deve criar um Novo Tópico e postar sua questão, seguindo todas as Regras