Paralelepípedo

Seja o paralelepípedo retangular ABCD-EFGH cujo volume é 320 e TR=RD. Calcule o volume do poliedro MTRSB-QLHGF mostrado.


a)240
b)280
c)144
d)160
e)204

R:a

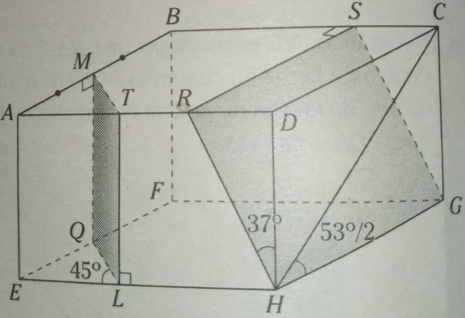
Sejam AD = a , AB = b m AE = h ---> V = a.b.h = 320 ---> I

Seja TR = RD = x ---> AT = AM = EL = EQ = a - 2.x ---> II

cos53º = 0,6 e sen53º = 0,8 ---> calcule sen(53º/2) , cos(53º/2) e tg(53º/2)

tg(53º/2) = GC/GH --> tg(53º/2) = h/b ---> III

tg37º = RD/DH ---> 0,6 = x/h ---> x = 0,6.h ---> IV

Calcule volume dos prismas v1 = AMT-EQL e v2 = HDR-GCS 

Volume procurado = V - v1 - v2

outro modo.


Considerando o triângulo HDR e lembrando dos ângulos agudos no pitagórico mais famoso, o 3-4-5, podemos seguramente estabelecer a seguinte proporção nos segmentos: DH = 4k e DR = 3k.
Lembrando também que a relação 1 : 2 nos catetos do triângulo nos fornece ângulo com exata metade daquele 4 : 3 pitagórico, e lembrando também que já temos CG = DH = 4k, podemos estabelecer que HG = 8k.
Desta forma, no desenho, AM= MB = 4k.
Assim as dimensões do paralelepípedo ficam 10k, 8k e 4k.
O resto está na figura.

Acho que não ficou bem explicado porquê a relação 1:2 nos catetos fornece um ângulo de exatamente 53°/2 daquele pitagórico primordial. Façamos isto agora.

Para facilitar contas, vamos considerar o pitagórico 6-8-10 (é simplesmente homotetia 2x do anterior) com ângulo reto em A, AB=6 e AC=8. Traçamos a ceviana BD tal que AD=3 (portanto DC=5).

Pela montagem, o ângulo A^BC=53°. Se BD for bissetriz teremos A^BD=53°/2 e verifica-se o teorema da bissetriz interna. A confirmar.

AD/AB = DC/BC -----> 3/6 = 5/10 .............. confirmado --> BD é bissetriz --> A^BD = 53°/2.

e um triângulo retângulo com um cateto o dobro do outro tem um ângulo de 53°/2 = 26,5°