Cinemática

Eu vou partir da ideia de que você não sabe nada de integrais, ok? Se você já conhece integrais, por favor, ignore boa parte do que eu vou dizer aqui.

Na minha resolução eu usei o cálculo integral pois estamos lidando com uma força variável, o que foge bastante dos problemas comuns do ensino médio, os quais trabalham majoritariamente com forças constantes.

De forma muito simplificada, a integral corresponde a área abaixo de uma curva. Por exemplo, digamos que a gente queira saber qual é a área abaixo da curva y=x no intervalo 1 ≤ x ≤ 5. Bom, uma forma de resolver esse exercício seria esboçar a curva y=x no sistema xOy e hachurar a área abaixo da curva y=x compreendida no intervalo 1 ≤ x ≤ 5, o que nos dá um trapézio e isso é fácil de ser calculado. Entretanto, e se fosse pedido para realizarmos o mesmo cálculo, porém, considerando a curva y=-(x-3)²+6? Aí complicaria pois a área abaixo dessa curva não é uma área trivial por assim dizer. Nisso seríamos obrigados a usar o cálculo integral para resolver o problema. Matematicamente falando, teríamos que calcular a integral de y=-(x-3)²+6 com os limites de integração indo de 1 até 5.

Algumas ilustrações:

Fig 01: Área abaixo da curva y=x, com 1 ≤ x ≤ 5:



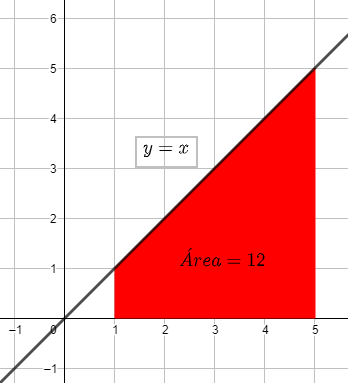
Matematicamente: [latex]\\\mathrm{A=\int_{1}^{5}(x)dx=12\ ou\ A=\frac{(5+1)\times 4}{2}=12}[/latex]

Fig 02: Área abaixo da curva y=-(x-3)²+6, com 1 ≤ x ≤ 5:



Matematicamente: [latex]\\\mathrm{A=\int_{1}^{5}\left [ -(x-3)^2+6 \right ]dx=\frac{56}{3}}[/latex]

Quanto ao nosso exercício, inicialmente temos a função y=√(-x²+20x), o que corresponde a uma semicircunferência, já que a raiz de índice par condiciona y ≥ 0. Isso facilita muito a nossa vida já que sabemos que a integral corresponde a área abaixo de uma curva, ou seja, desse modo não precisaremos calcular a integral propriamente dita, mas sim a área abaixo de uma curva facilmente reconhecida. A curva y=√(-x²+20x) está definida para 0 ≤ x ≤ 20 e 0 ≤ y ≤ 10, logo, temos uma semicircunferência de raio 10.

Fig 03: Área abaixo da curva y=√(-x²+20x) para 0 ≤ x ≤ 20 e 0 ≤ y ≤ 10:



Portanto, a integral abaixo corresponde a área de uma semicircunferência de raio 10.

[latex]\\\mathrm{\tau =\int F(x)dx=\int_{0}^{20}\left (\sqrt{-x^2+20x} \right )dx=\frac{1}{2}\times \pi \times (10)^2=50\times \pi\ J}\\\\\mathrm{Mas,\ \tau=\Delta E_C=\frac{1}{2}\times m\times v^2\to v=\sqrt{\frac{2\times 50\times \pi }{4}}=5\times \sqrt{\pi }\ m\times s^{-1}}[/latex]

Se você tiver dúvidas quanto ao cálculo da integral, avise. A propósito, a integral que eu cheguei também pode ser resolvida por substituição trigonométrica. Não o fiz desse jeito porque eu acho que dessa forma foge-se muito do escopo do que é cobrado no ensino médio ou pré-universitário e também porque é um esforço desnecessário. Se você quiser, depois eu posto algo por substituição trigonométrica. No mais, acho que é isso.