Sistema Lineares

por Tsuki Mikan Ter 16 Nov 2021, 09:32

O sistema de equações lineares 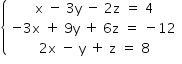Sistema Lineares Showimage

A

tem infinitas soluções.
B

só tem a solução trivial.
C

não possui solução.
D

admite a solução (1, 1, -3).
E

admite a solução (2, -1, 4).

por **qedpetrich** Ter 16 Nov 2021, 10:35

Olá Tsuki Mikan;

Multiplicando a primeira equação por -3, temos o seguinte:

$Sistema Lineares Gif$

Ou seja, temos a mesma equação (compare com a segunda). Portanto, fica evidente que o sistema exposto possui duas equações e três incógnitas, caracterizando um sistema que não possui solução.

Espero ter ajudado!

por **Rory Gilmore** Ter 16 Nov 2021, 11:42

O argumento utilizado está incorreto, por exemplo, no sistema
x + y + z = 3
2x + 2y + 2z = 6
y = 4

a segunda equação é um múltiplo da primeira, mas ele possui infinitas soluções da forma (-z - 1, 4, z).

Na verdade, para resolver o sistema devemos utilizar o escalonamento, aplicando esse método chegamos em uma matriz aumentada da forma
- 3 9 6 12
0 5 5 0
0 0 0 0

Assim, o sistema possui 2 pivôs e uma variável livre. Portando, possui infinitas soluções, que são dadas resolvendo em função de z o sistema
-3x + 9y + 6z = 12
5y + 5z = 0