Cilindro de revolução
2 participantes
Página 1 de 1
 Cilindro de revolução
Cilindro de revolução
deduza uma equação do cilindro de revolução gerado pela rotação da reta r em torno da reta s, sendo:
r:
x = 2
y = 3
z = t
s:
x = 3
y = 0
z = t
Resposta: (x - 3)^2 + y^2 = 10
Quem puder fazer o passo a passo eu agradeço.
r:
x = 2
y = 3
z = t
s:
x = 3
y = 0
z = t
Resposta: (x - 3)^2 + y^2 = 10
Quem puder fazer o passo a passo eu agradeço.
Starsec77- Iniciante
- Mensagens : 1
Data de inscrição : 04/02/2021
 Re: Cilindro de revolução
Re: Cilindro de revolução
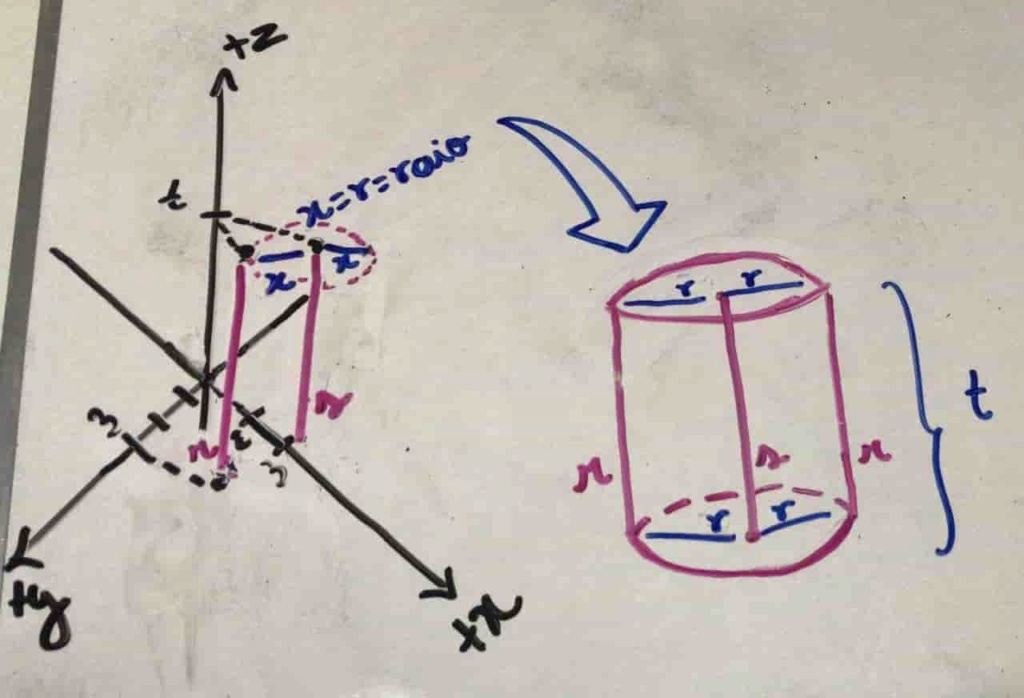
1. Inicialmente, desenhei o plano cartesiano xyz (colocarei na próxima mensagem) e juntei os pontos para observar melhor a situação e ver como poderíamos fazer a equação;
2. Depois, deve-se perceber que a altura do cilindro será t e, como é a mesma para os dois segmentos de reta, nós temos uma base invariável na altura, consegue notar? Logo, o nosso trabalho será de apenas de construir uma equação para os pontos xy da base, pois z será t e constante;
3. Agora, nota-se mais uma coisa: a base do cilindro é uma circunferência e, portanto, utilizarei a fórmula dessa:
(x-xo)² + (y-y0)²= R², sendo x0 e y0 os pontos centrais da base e x e y, pontos quaisquer;
4. Substitui-se x e y pelos pontos do segmento de reta r, pois a distância entre esses e o centro define o raio:
(2-3)² + (3-0)²= R²
1 + 9= R²
R²= 10
5. Por fim, já temos o que é preciso para formar a equação, que são os valores da incógnitas fixas, pois o raio sempre será 10 e os pontos centrais sempre serão (3,0,t):
(x-x0)² + (y-y0)²= R²
(x-3)² + (y)²= 10
Pronto! A equação desse cilindro poderá ser representada assim.
Se precisar esclarecer algo melhor, me avise
2. Depois, deve-se perceber que a altura do cilindro será t e, como é a mesma para os dois segmentos de reta, nós temos uma base invariável na altura, consegue notar? Logo, o nosso trabalho será de apenas de construir uma equação para os pontos xy da base, pois z será t e constante;
3. Agora, nota-se mais uma coisa: a base do cilindro é uma circunferência e, portanto, utilizarei a fórmula dessa:
(x-xo)² + (y-y0)²= R², sendo x0 e y0 os pontos centrais da base e x e y, pontos quaisquer;
4. Substitui-se x e y pelos pontos do segmento de reta r, pois a distância entre esses e o centro define o raio:
(2-3)² + (3-0)²= R²
1 + 9= R²
R²= 10
5. Por fim, já temos o que é preciso para formar a equação, que são os valores da incógnitas fixas, pois o raio sempre será 10 e os pontos centrais sempre serão (3,0,t):
(x-x0)² + (y-y0)²= R²
(x-3)² + (y)²= 10
Pronto! A equação desse cilindro poderá ser representada assim.
Se precisar esclarecer algo melhor, me avise

fernandalnh- Recebeu o sabre de luz

- Mensagens : 132
Data de inscrição : 02/02/2021
Idade : 22
Localização : Macapá, AP
 Re: Cilindro de revolução
Re: Cilindro de revolução
fernandalnh escreveu:1. Inicialmente, desenhei o plano cartesiano xyz (colocarei na próxima mensagem) e juntei os pontos para observar melhor a situação e ver como poderíamos fazer a equação;
2. Depois, deve-se perceber que a altura do cilindro será t e, como é a mesma para os dois segmentos de reta, nós temos uma base invariável na altura, consegue notar? Logo, o nosso trabalho será de apenas de construir uma equação para os pontos xy da base, pois z será t e constante;
3. Agora, nota-se mais uma coisa: a base do cilindro é uma circunferência e, portanto, utilizarei a fórmula dessa:
(x-xo)² + (y-y0)²= R², sendo x0 e y0 os pontos centrais da base e x e y, pontos quaisquer;
4. Substitui-se x e y pelos pontos do segmento de reta r, pois a distância entre esses e o centro define o raio:
(2-3)² + (3-0)²= R²
1 + 9= R²
R²= 10
5. Por fim, já temos o que é preciso para formar a equação, que são os valores da incógnitas fixas, pois o raio sempre será 10 e os pontos centrais sempre serão (3,0,t):
(x-x0)² + (y-y0)²= R²
(x-3)² + (y)²= 10
Pronto! A equação desse cilindro poderá ser representada assim.
Se precisar esclarecer algo melhor, me avise

fernandalnh- Recebeu o sabre de luz

- Mensagens : 132
Data de inscrição : 02/02/2021
Idade : 22
Localização : Macapá, AP
 Tópicos semelhantes
Tópicos semelhantes» Cilindro de revolução.
» Cilindro de revolução
» (ITA) Cilindro de Revolução
» Cilindro de revolução
» Cilindro dee revolução
» Cilindro de revolução
» (ITA) Cilindro de Revolução
» Cilindro de revolução
» Cilindro dee revolução
Página 1 de 1
Permissões neste sub-fórum
Não podes responder a tópicos












