Geometria Espacial

por Deltz Ter 09 Fev 2021, 12:29

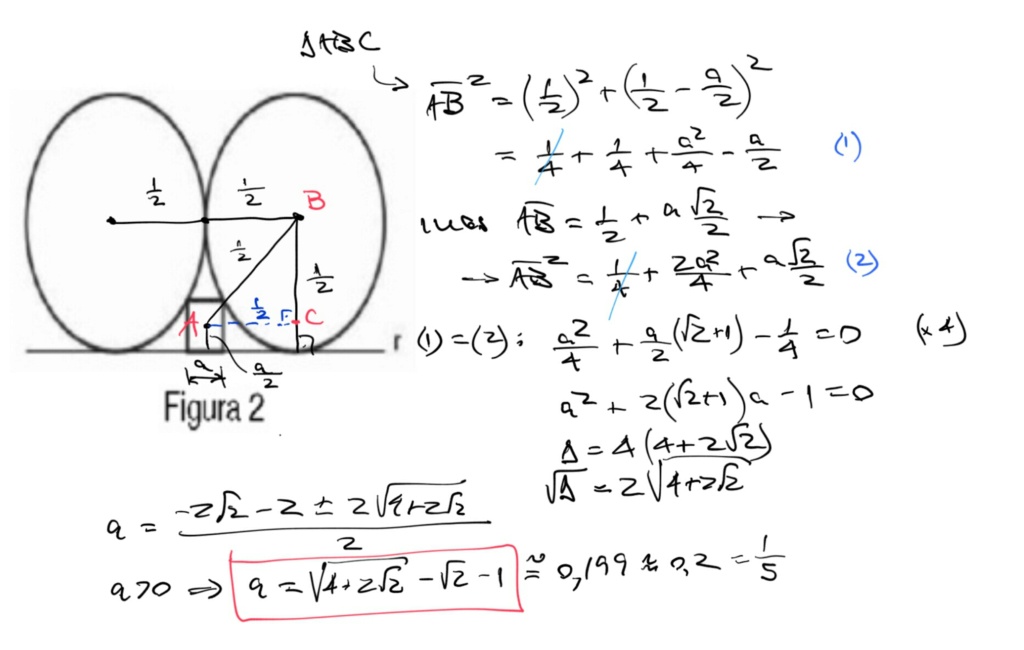
Para armazenar um conjunto de canos idênticos (Figura 1), de 20 dm de comprimento, com formato de um cilindro circular reto, um engenheiro colocou entre um cano e outro uma peça de borracha com formato de um prisma reto de base quadrada. Externamente, cada cilindro tem 1 dm de diâmetro dabase. A Figura 2 a seguir representa a vista de frente do projeto desse engenheiro.

No projeto, as bases desses cilindros são representadas por circunferências que são tangentes entre si e tangenciam a linha r que representa o solo. Um dos lados do quadrado que representa a base do prisma reto está sobre a reta r que representa o solo e os dois vértices opostos a esse lado pertencem,cada um, a uma das circunferências.

Assinale a alternativa que apresenta, corretamente, a medida do lado do quadrado.

A)1/5 dm B)2/5 dm C)1/2 dm D)1/raiz quadrada de 2 dm E)2/raiz quadrada de 3 dm

Gabarito : A

por **Medeiros** Ter 09 Fev 2021, 15:28

por Deltz Ter 09 Fev 2021, 16:29

Obrigado Medeiros por resolver essa questão tenho muita dificuldade em matemática.

por **Elcioschin** Ter 09 Fev 2021, 17:20

Outra solução, com r = 5 cm

por Deltz Ter 09 Fev 2021, 18:07

Obrigado Elcioschin.

por **Medeiros** Ter 27 Abr 2021, 13:38

ATENÇÃO: a resposta que dei acima está ERRADA, percebi somente hoje. Mais tarde posto a resolução correta.

por **Medeiros** Ter 27 Abr 2021, 18:46

Minhas sinceras desculpas ao Deltz mas minha resposta anterior tem um erro crasso -- infelizmente agora não consigo colocar um alerta nela -- veja na figura abaixo.

O erro foi supor que o prolongamento do raio coincidia com a diagonal do quadrado. Isto somente seria válido se o quadrado ficasse inteiramente dentro do quadrante da circunferência, o que não é o caso desta questão.

Mas vamos supor que em vez de um único quadrado tenhamos dois quadradinhos de aresta a cada um dentro do respectivo quadrante da circunferência. Eles cumprem a mesma função que o quadrado grande (aresta x) e para isto precisam ocupar uma determinada área entre os canos. Sabemos que o quadrilátero que mantém uma mesma área dada com o menor perímetro é o quadrado. Então o pedido lado do quadrado será: x = a.√2.