Pontos notáveis

por pedropand Ter 04 Ago 2020, 20:29

Olá!

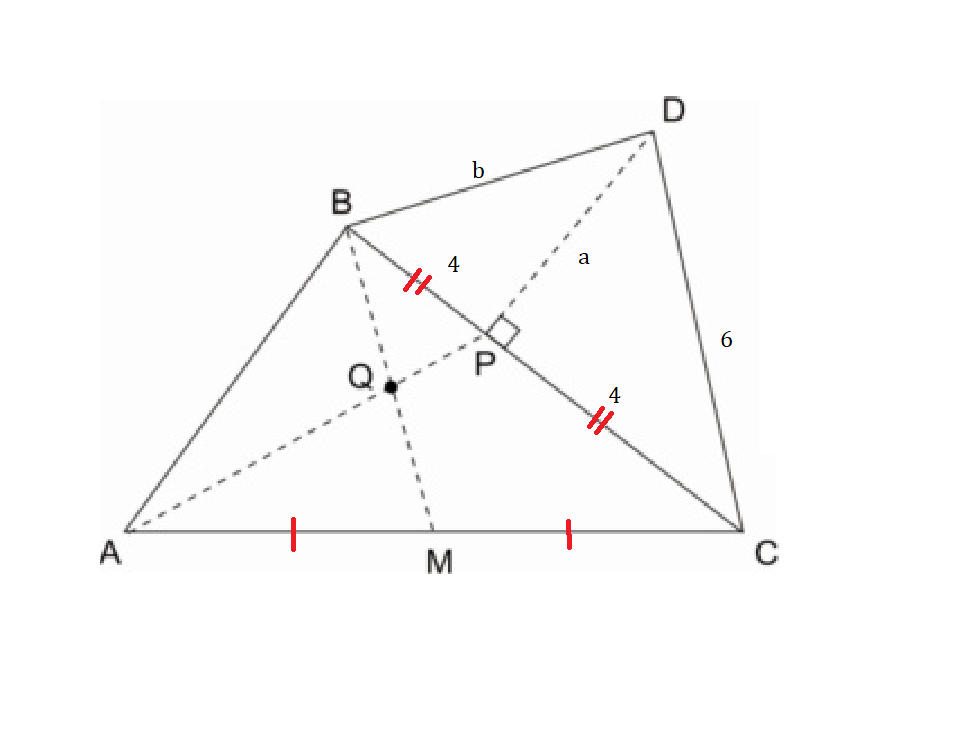
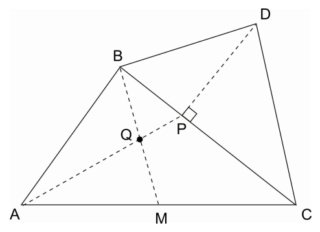
Ibmec/08: Na figura ao lado, feita fora de escala, considere os triângulos ABC e BCD. M é o ponto do lado AC, P é o ponto do lado BC tal que os segmentos BC e DP são perpendiculares, e Q é o ponto onde os segmentos BM e AP interceptam-se. Sabendo que AM=MC, BQ=2*QM, CD=6cm, BP=4cm, pode-se concluir que o perímetro do triângulo BCD, em centímetros, vale: Gabarito: 20cm

Agradeço!

por **Rory Gilmore** Ter 04 Ago 2020, 20:39

Q é baricentro do triângulo ABC, logo AP é mediana.

Aplicando o Teorema de Pitágoras nos triângulos BPD e CPD:
(6)² = a² + (4)²
36 = a² + 16
a² = 20

b² = (4)² + a²
b² = 16 + 20
b² = 36
b = 6 cm

Perímetro:
6 + 8 + 6 = 20 cm.

por pedropand Ter 04 Ago 2020, 21:45

Não entendi como você concluiu que o ponto Q é o baricentro.

por **Rory Gilmore** Ter 04 Ago 2020, 22:11

O baricentro de um triângulo é o ponto de encontro de suas medianas. O baricentro divide cada mediana em duas partes de tal forma que a parte que contém o vértice é o dobro da outra parte.

Na mediana BM temos:
BQ = parte que contém o vértice
QM = parte que não contém o vértice.
BQ = 2.QM

Por isso Q é baricentro.