Romênia 1974
2 participantes
PiR2 :: Questões Especiais :: Olimpíadas :: Matemática
Página 1 de 1
Romênia 1974
por Barbaducki Dom 15 Set 2019, 20:34
Seja a, b e c parâmetros reais e positivos. Resolva a equação:
√(a + bx) + √(b + cx) + √(c + ax) = √(b - ax) + √(c-bx) + √(a - cx)
Gabarito: x = 0 é a única raiz
√(a + bx) + √(b + cx) + √(c + ax) = √(b - ax) + √(c-bx) + √(a - cx)
Gabarito: x = 0 é a única raiz
Barbaducki- Recebeu o sabre de luz
- Mensagens : 119
Data de inscrição : 14/04/2019
Idade : 25
Localização : Rio de Janeiro
Ideia para resolver a questão
por NikolsLife Ter 10 Dez 2019, 15:53
Isso é equivalente a:
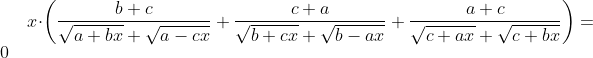implicando 
A ideia principal é a conjugação
A ideia principal é a conjugação
NikolsLife- Padawan
- Mensagens : 84
Data de inscrição : 10/12/2019
Tópicos semelhantes» Romênia - Ângulo de 90º
» Romênia 2017 - Indução finita (?)
» Olimpíada da Romênia(2006) - Circunferência
» Indução - Romênia 2017
» (Romênia) Segmentos do triângulo
» Romênia 2017 - Indução finita (?)
» Olimpíada da Romênia(2006) - Circunferência
» Indução - Romênia 2017
» (Romênia) Segmentos do triângulo
PiR2 :: Questões Especiais :: Olimpíadas :: Matemática
Página 1 de 1
Permissões neste sub-fórum
Não podes responder a tópicos
