Quantidade de movimento e sua conservação

Na situação representada na figura a seguir, dois pequenos blocos, 1 e 2, de massas iguais a 2,0 kg encontram-se em repouso no ponto B de uma calha circular de raio R, perfeitamente lisa, contida em um plano vertical. No local, a influência do ar é desprezível e adota-se g = 10 m/s².


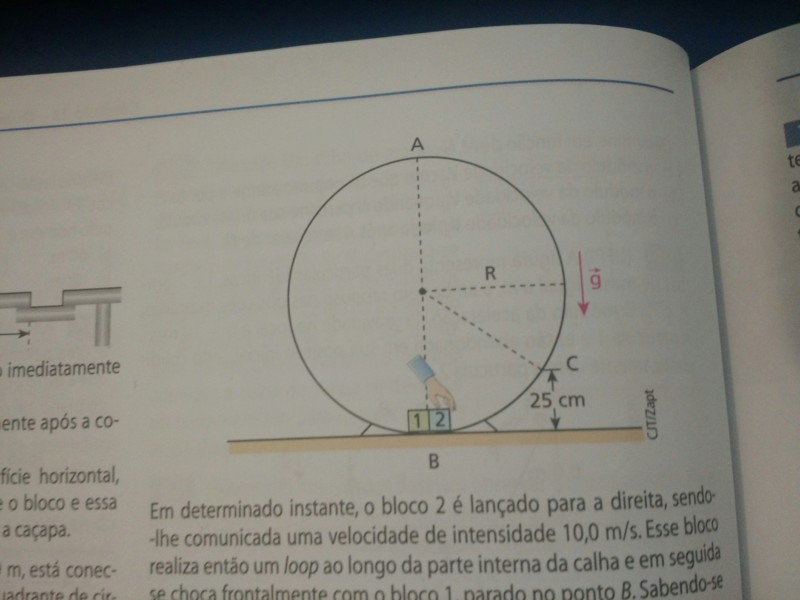
Em determinado instante, o bloco 2 é lançado para a direita, sendo-lhe comunicado uma velocidade de intensidade igual a 10 m/s. Esse bloco realiza então um loop ao longo da parte interna da calha e em seguida se choca frontalmente com o bloco 1, parado no ponto B. Sabendo-se que após a colisão os blocos permanecem unidos e que ao passarem no ponto A eles não trocam forças com a calha, pede-se calcular:
a) O valor de R em centímetros;
b) A intensidade da força de contato trocada entre o bloco 2 e a calha na sua primeira passagem no ponto C.
GABARITO:
a) R = 50 cm
b) 390 N
*Eu resolvi de uma maneira errada, mas não sei aonde estou errando, alguém poderia me ajudar?
Fiz do seguinte modo...
Fcp = P
mv²/R = mg
mv² = mgR
v² = gR
v² = 10R
Pela conservação de energia mecânica:
Emi = Emf
mv²/2 = mv'²/2 + mg × 2R
v²/2 = v'²/2 + 20R
10²/2 = 10R/2 + 20R
50 = 5R + 20R
25R = 50
R = 2 m = 200 cm
Outra pergunta que tenho em mente é...
A força centrípeta é uma força externa ou interna?*

Bom, a resposta saiu errada porque você considerou a energia cinética inicial como a energia cinética inicial de um só bloco. Veja bem, a questão nos diz que, após a colisão, os dois blocos chegam ao topo da calha sem trocar forças com a mesma. Portanto, realmente, a Fcp dos DOIS blocos será igual ao peso dos DOIS blocos, assim como você fez:

a) Fcp(sistema) = Fp(sistema) ---> (m1 + m2)v²/R = (m1 + m2)g

Podemos cancelar as massas:

v²/R = g ---> v² = Rg

Esta é a velocidade do conjunto, dos DOIS blocos no topo do looping.

Agora, pela conservação da energia mecânica:

Em(i)(sistema) = Em(f)(sistema), e o sistema é composto pelos dois blocos. Considerando a base da rampa como a altura 0, teremos apenas a energia cinética dos DOIS blocos no início, e como eles saem juntos após o choque, os dois terão as mesmas velocidades:

(m1 + m2)v²(i)/2 = (m1 + m2)v²/2 + (m1 + m2)g2R

Cancelando as massas novamente, e multiplicando a equação por dois temos:

v²(i) = v² + 4Rg

Esta velocidade inicial, é a velocidade imediatamente após a colisão do bloco 2 com o bloco 1, que saem juntos. Por isso, não podemos considerar a velocidade inicial apenas do bloco B. Ele realmente termina o looping e volta pra base com a mesma velocidade com a qual saiu, mas após o choque a velocidade do conjunto muda.
Admitindo nula as forças externas, podemos aplicar a conservação da quantidade de movimento do sistema, antes e depois do choque:

Q(i)(sistema) = Q(f)(sistema), como a quantidade de movimento do sistema é a soma da quantidade de movimento dos corpos que o compõe, e Q é o produto entre a massa do corpo e sua velocidade, temos:

Q(i)(A) + Q(i)(B) = Q(f)(A) + Q(f)(B) ---> m(A)*0 + m(B)*10 = m(A)v(A) + m(B)v(B)

Como sabemos as massas, e após o choque A e B se movem juntos, com a mesma velocidade, podemos dizer que:

2*10 = (m(A) + m(B))*v(f) ---> 20 = 4v(f) ---> v(f) = 5 m/s, bem diferente dos 10 m/s que o bloco B tem instantaneamente antes de atingir o bloco A.

Ou seja, depois da colisão, A e B passam a se mover juntos com velocidade de 5 m/s, e essa é a velocidade que devemos usar como velocidade da energia cinética inicial.
Agora podemos aplicar  em v²(i) = v² + 4Rg:

5² = v² + 4*R*10 ---> 25 = v² + 40R

Como sabemos que v² é Rg, temos:

25 = Rg + 40R ---> 25 = 10R + 40R ---> 25 = 50R ---> R = 0,5m, que corresponde a 50cm.

b) Agora queremos a força de contato entre o bloco B e a calha no ponto C, que está a 25 cm do solo. Vamos começar com energia neste ponto: 

Em(i) = Em(C) ---> Ec(i) = Ep(C) + Ec(C) ---> m(B)v²(i)/2 = m(B)v²(C)/2 + m(B)gh(C)

Podemos tirar as massas e colocar os valores conhecidos, e multiplicar a equação por dois:

10² = v²(C) + 2*10*0,25 ---> 100 - 5 = v²(C) ---> v²(C) = 95,0

Agora, colocamos as forças. No ponto C temos o peso, a normal (que é a força que queremos descobrir), e a resultante radial centrípeta.
Para encontrarmos as forças radiais, vamos ter que decompor a força peso, e para isso, temos que descobrir o ângulo que ela faz:


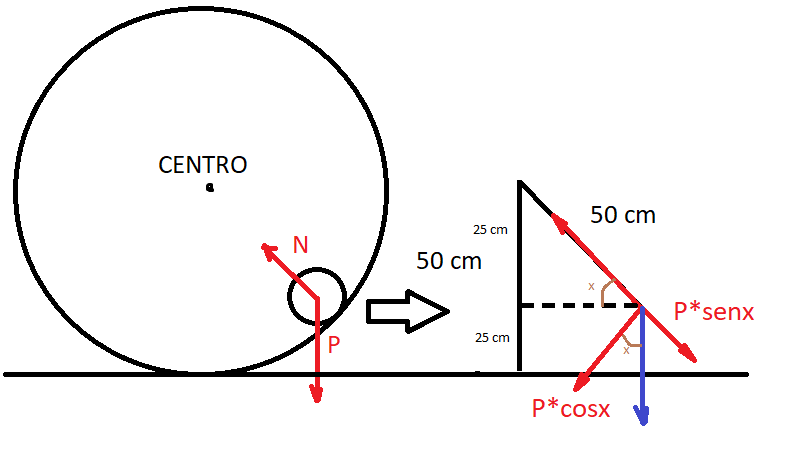
Como o total do raio é 50 cm, e já subimos 25 cm, então sobram 25 cm. Decompondo a força peso nas respectivas direções, podemos ver que os ângulos em marrom são iguais. Mas quanto eles valem?
O triângulo feito pelo raio e pelo resto do raio é retângulo, e tem lados 50 cm e 25 cm, logo, podemos dizer que:

sen x = 25/50 = 1/2, ou seja, x vale 30º. Mas o importante mesmo é agora. Depois de decompor a força peso, vemos que uma parcele dela está na direção radial, e ela vale o próprio peso vezes o seno do ângulo encontrado. Logo, a parcela radial do peso é:

m(B)*g*sen x = 2*10*1/2 = 10 N
Quer dizer que dos 20 newtons de peso, 10 ficam na direção do raio.
Agora podemos descobrir a outra força em vermelho, que é a força normal. Como a resultante no movimento circular na direção do raio é a centrípeta, temos:

Fcp = N - P*sen x ---> m(B)v²(C)/R = N + 10, aqui temos N - P pois a resultante deve apontar para o centro da circunferência, logo, vemos que N deve ser maior que P*sen x; e como as forças têm sentido contrário, fazemos uma subtração.
Como sabemos que v²(C) = 95,0, e R = 0,5m:

2*95/0,5 = N - 10 --->380 = N - 10 ---> N = 390 newtons



Quanto à parte da força centrípeta ser uma força interna ou externa, mesmo após eu admitir que consideramos as forças externas nulas, você me pegou nesta pergunta. Nunca parei para analisar isso, e realmente não sei. Pelo que eu entendo, uma força externa não é capaz de variar a quantidade de movimento do sistema, já a interna é, como por exemplo a força que um bloco trocou com o outro durante a colisão. Essas forças são internas, e têm mesmo módulo para os dois corpos. 
Vamos esperar para que outra pessoa possa explicar e tirar essa nossa dúvida.

Mas em relação ao que eu soube resolver, você entendeu? Qualquer dúvida não hesite em perguntar!