Álgebra linear-Autovalores

por **alansilva** 28/1/2019, 11:13 am

Determine os autovalores e uma base para os respectivos autoespaços da seguinte matriz:

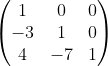
$Álgebra linear-Autovalores Gif$

por Gabriel Trindade 11/2/2019, 1:34 pm

Olá. Podemos começar com a definição de auto-vetor:

M~\vec{v}=\lambda~\vec{v}

Onde M é a matriz dada e \lambda é um escalar. Assim, se I é a matriz identidade:

\vec{v}.(M-\lambda.I)=\vec{0}~~(Eq. 1)

Vamos garantir que M-\lambda.I é não invertível, de forma que garantimos que exista \vec{v} \neq \vec{0}.

det(M-\lambda.I)=0
(1-\lambda)^{3}=0
\lambda=1

Logo, \lambda=1 é o único auto-valor de M

Vamos substituir, agora, o auto-valor na equação 1 (obs: \vec{v}=(v_1,v_2,v_3), numa base do espaço tridimensional que estamos trabalhando):

\begin{bmatrix}
1-1 & 0 & 0\\
-3 & 1-1 & 0\\
4 & -7 & 1-1
\end{bmatrix} . \begin{bmatrix}
v_1 \\
v_2 \\
v_3
\end{bmatrix} = \vec{0}}

Assim, temos o sistema:

\left\{\begin{matrix}
0&=0\\
-3.v_1&=0 \\
4.v_1-7.v_2& =0
\end{matrix}\right.

Da segunda equação, tiramos que v_1=0 e, da terceira, que v_2=0. Assim, v_3 pode assumir o valor de qualquer escalar. Dessa forma:

\vec{v}=v_3. (0,0,1)

Logo, uma base pro auto-espaço de \lambda=1 é:

\mathfrak{B}( 1)=(0,0,1)

Espero que esteja certo e que tenha ajudado!!!

Álgebra linear-Autovalores

Álgebra linear-Autovalores

Re: Álgebra linear-Autovalores

Um fórum livre e democrático.