Raízes complexas
3 participantes
PiR2 :: Matemática :: Álgebra
Página 1 de 1
Raízes complexas
por Victor Luz Seg 28 maio 2018, 22:34
Determine as raízes quadradas de 4+4i√3
- gabarito:
- ±(√6+i√2)
Última edição por Victor Luz em Ter 29 maio 2018, 14:02, editado 1 vez(es)
Victor Luz- Mestre Jedi
- Mensagens : 775
Data de inscrição : 14/03/2017
Idade : 27
Localização : São Paulo - Brasil
Re: Raízes complexas
por Lucas Pedrosa. Seg 28 maio 2018, 23:26
Transformei para a forma trigonométrica:
\\|Z| = \sqrt{(4)^{2}+(4\sqrt{3})^{2}} = 8\\\\cos\theta =\frac{4}{8}=\frac{1}{2};\;sen\theta =\frac{4\sqrt{3}}{8}=\frac{\sqrt{3}}{2};\;\theta =\frac{\pi }{3}\\\\Z=8cis(\frac{\pi }{3})\\\\\sqrt{Z}=\sqrt{8}cis(\frac{\frac{\pi }{3}+2k\pi }{2})\\\\k=0\rightarrow \sqrt{Z}= 2\sqrt{2}(\frac{\sqrt{3}}{2}+i\frac{1}{2})=\sqrt{6}+i\sqrt{2}\\\\k=1\rightarrow \sqrt{Z}=2\sqrt{2}(-\frac{\sqrt{3}}{2}-i\frac{1}{2})=-\sqrt{6}-i\sqrt{2}
Lucas Pedrosa.- Matador
- Mensagens : 331
Data de inscrição : 25/01/2017
Idade : 27
Localização : NATAL - RN
Re: Raízes complexas
por RodrigoA.S Seg 28 maio 2018, 23:40
OBS: Postei só pelo tempo fazendo mesmo hehe, a solução do Lucas já está perfeita.
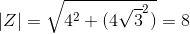
Para encontrar teta basta saber que o cosseno do argumento vale a parte real dividia pelo módulo e que seno vale a parte imaginária dividida pelo módulo.
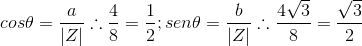
cos vale 1/2 e sen V3/2 então esse ângulo só pode ser do primeiro quadrando e vale 60º.
Como n vale 2 pois a questão pede raiz quadrada, iremos variar k=0,1(antes de dar uma volta completa e dando uma volta completa).
Para K=0
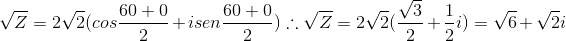
Para K=1
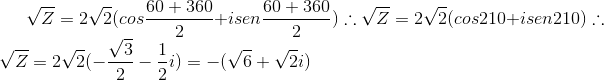
Portanto, temos as raízes :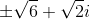
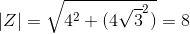
Para encontrar teta basta saber que o cosseno do argumento vale a parte real dividia pelo módulo e que seno vale a parte imaginária dividida pelo módulo.
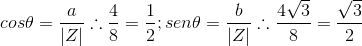
cos vale 1/2 e sen V3/2 então esse ângulo só pode ser do primeiro quadrando e vale 60º.
Como n vale 2 pois a questão pede raiz quadrada, iremos variar k=0,1(antes de dar uma volta completa e dando uma volta completa).
Para K=0
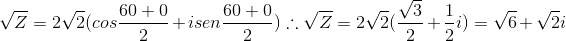
Para K=1
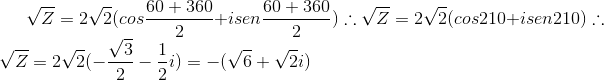
Portanto, temos as raízes :
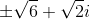
RodrigoA.S- Elite Jedi
- Mensagens : 449
Data de inscrição : 12/07/2017
Idade : 25
Localização : Nova Iguaçu
Tópicos semelhantesPiR2 :: Matemática :: Álgebra
Página 1 de 1
Permissões neste sub-fórum
Não podes responder a tópicos
