Dimensões

por PlodX Sex 17 Jun 2011, 19:54

Dentre todos os retângulos de perímetro 20 cm, determine as dimenções daquele que tem área máxima.

por mcgiorda Sex 17 Jun 2011, 20:56

20 cm de perímetro...

opções (dimensões):

1x9
2x8
.
.
.
5x5
.
.
.
9x1

Sabemos que o pico será 5x5;

Sempre que temos um número x e sabemos que:

a+b = x

para a.b assumir o valor máximo, então teremos que escolher o menor módulo entre esses números, que seria a = b, ou, se x é ímpar, a = b-1 ou vice e versa.

Portanto:

Máx área:

l² = 5² = 25 cm²

por **Euclides** Sex 17 Jun 2011, 21:23

Muito bom mcgiorda, porém isso também pode ser resolvido com uma função do segundo grau:

$\dpi{120} \\P=2(a+b)\hspace{50}A=a.b\\\\a=\frac{P}{2}-b\hspace{60}A=\frac{Pb}{2}-b^2$

a função acima dá a área em função de um dos lados. Calcule o máximo da função e encontre o lado do retângulo (que é um quadrado).

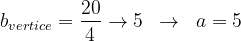
$\dpi{120} b_{vertice}=\frac{20}{4}\to 5\;\;\to\;\;a=5$

por **abelardo** Sáb 18 Jun 2011, 00:49

No livro ''Elementos'' de Euclides existe alguma coisa falando sobre o quadrado ser entre os retângulos, de um mesmo perímetro, o de maior área?

por **Euclides** Sáb 18 Jun 2011, 01:22

Acho que não. O "Elementos" estabelece as bases da Geometria.

por MuhRod Seg 10 Out 2022, 10:30

A partir da informação do perímetro do retângulo igual a 20 CM, sabemos que:

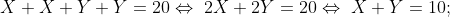
$Dimensões Png$
(SENDO X E Y OS RESPECTVIVOS LADOS DO RETÂNGULO)

SABEMOS QUE A ÀREA DO RETÂNGULO É ORIGINALIZADA PELO PRODUTO ENTRE A BASE E ALTURA:
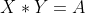
$Dimensões Png$
(CHAMAMOS DE A O RESULTADO DA ÁREA)

ENTRETANTO, TEMOS 3 VARIÁVEIS NESTA FÓRMULA, ENTÃO VAMOS SUBSTIUIR UMA:
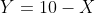
$Dimensões Png$
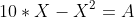
$Dimensões Png$
$Dimensões Png$

COMO QUEREMOS O MAIOR VALOR DA ÀREA E ASTAMOS ANTE UMA FUNÇÃO QUADRÁTICA, BASTA CALCULAR O VALOR MÁXIMO DE A( SENDO QUE A<0, CONCAVIDADE DA PARÁBOLA PARA BAIXO)
[latex]Am=-\triangle/4a[/latex]
[latex]Am=-(b^{2}-4ac)/4a[/latex]
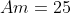
$Dimensões Png$

POR TANTO, 25 CM2 É A MAIOR ÁREA POSSÍVEL.

por **Elcioschin** Seg 10 Out 2022, 10:38

O enunciado não pediu o valor da área máxima: ele pediu as dimensões do retângulo:

A = - x² + 10.x --> Vértice: x = - b/2.a ---> x = - 10/2.(-1) ---> x = 5

y = 10 - x ---> y = 5

Dimensões x = y = 5