Raízes - Polinômio
2 participantes
PiR2 :: Matemática :: Álgebra
Página 1 de 1
 Raízes - Polinômio
Raízes - Polinômio
Calcule todas raízes do polinômio = x^{4}+x^{3}+x^{2}+ x + 1) sabendo que este divide o polinômio
sabendo que este divide o polinômio 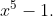

Fafa- Grupo
Velhos amigos do Fórum
- Mensagens : 497
Data de inscrição : 31/07/2009
Localização : Rio de Janeiro
 Re: Raízes - Polinômio
Re: Raízes - Polinômio
Hola Fafa.
Veja a solução do nosso grande moderador Elcio:
Este é "complexo"
x^5 - 1 = (x - 1)*(x^4 + x³ + x² + x + 1) ---> x^5 - 1 = (x - 1)*p(x) --->Todas as raízes de p(x) são também raízes de x^5 - 1
Uma das raízes de x^5 - 1 = 0 é x = 1
x^5 - 1 = 0 ----> x^5 = 1 ---> x^5 = cos0 + i*sen0
x = cos(k*360º/5) + i*sen(k*360º/5) ----> x = cos(k*72º) + i*sen(k*72º)
Para k = 0 ----> x = 1 ----> Já sabíamos
Para k = 1 ----> x = cos72º + i*sen72º ----> x = (V5 - 1)/4 + i*(V5 + 1)/4
Para k = 2 ----> x = cos144º + i*sen144 ----> x = - (V5 + 1)/4 + i*V(10 - V20)/4
Para k = 3 e k = 4 nem é preciso fazer as contas, pois as raízes complexas conjugadas também são raízes:
As 4 raízes são:
(V5 - 1)/4 + i*(V5 + 1)/4
(V5 - 1)/4 - i*(V5 + 1)/4
- (V5 + 1)/4 + i*V(10 - V20)/4
- (V5 + 1)/4 - i*V(10 - V20)/4
Veja a solução do nosso grande moderador Elcio:
Este é "complexo"
x^5 - 1 = (x - 1)*(x^4 + x³ + x² + x + 1) ---> x^5 - 1 = (x - 1)*p(x) --->Todas as raízes de p(x) são também raízes de x^5 - 1
Uma das raízes de x^5 - 1 = 0 é x = 1
x^5 - 1 = 0 ----> x^5 = 1 ---> x^5 = cos0 + i*sen0
x = cos(k*360º/5) + i*sen(k*360º/5) ----> x = cos(k*72º) + i*sen(k*72º)
Para k = 0 ----> x = 1 ----> Já sabíamos
Para k = 1 ----> x = cos72º + i*sen72º ----> x = (V5 - 1)/4 + i*(V5 + 1)/4
Para k = 2 ----> x = cos144º + i*sen144 ----> x = - (V5 + 1)/4 + i*V(10 - V20)/4
Para k = 3 e k = 4 nem é preciso fazer as contas, pois as raízes complexas conjugadas também são raízes:
As 4 raízes são:
(V5 - 1)/4 + i*(V5 + 1)/4
(V5 - 1)/4 - i*(V5 + 1)/4
- (V5 + 1)/4 + i*V(10 - V20)/4
- (V5 + 1)/4 - i*V(10 - V20)/4

Paulo Testoni- Membro de Honra

- Mensagens : 3409
Data de inscrição : 19/07/2009
Idade : 77
Localização : Blumenau - Santa Catarina
 Tópicos semelhantes
Tópicos semelhantes» Raízes do polinômio
» Raízes do polinômio
» Raízes polinômio
» Polinômio e raízes
» Polinômio - (raízes)
» Raízes do polinômio
» Raízes polinômio
» Polinômio e raízes
» Polinômio - (raízes)
PiR2 :: Matemática :: Álgebra
Página 1 de 1
Permissões neste sub-fórum
Não podes responder a tópicos












