Dizima periódica
+2
JoaoGabriel
Fafa
6 participantes
PiR2 :: Matemática :: Álgebra
Página 1 de 2
Página 1 de 2 • 1, 2 
 Dizima periódica
Dizima periódica
Suponha que você esteja em sala de aula, explicando aos seus alunos, como se determina:
A fração irredutível que é igual a 3,188181818181........
A fração irredutível que é igual a 3,188181818181........

Fafa- Grupo
Velhos amigos do Fórum
- Mensagens : 497
Data de inscrição : 31/07/2009
Localização : Rio de Janeiro
 Re: Dizima periódica
Re: Dizima periódica
Olá Fafá!
Se for uma dízima periódica, acho que digitou errado,pondo um 8 a mais Veja:
A fração irredutível que é igual a 3,188181818181........
Acho que o certo seria 3,18181818181........
Assim sendo, vou tentar:
3,1818... = 3 + 0,1818...
0,1818... pode ser entendido como 0,18 + 0,0018 + 0,0000018..., ou seja, é a soma de infinitos termos de uma PG de razão 0,01.
Assim:
Sn = a1/1-q
Sn = 0,18/1 - 0,01
Sn = 0,18/0,99
Sn = 18/99 = 2/11
Logo:
3 + 2/11 .:.
(33 + 2)/11
Resposta: 35/11
Acho que é isso, se não for avisem, abraços
Se for uma dízima periódica, acho que digitou errado,pondo um 8 a mais Veja:
A fração irredutível que é igual a 3,188181818181........
Acho que o certo seria 3,18181818181........
Assim sendo, vou tentar:
3,1818... = 3 + 0,1818...
0,1818... pode ser entendido como 0,18 + 0,0018 + 0,0000018..., ou seja, é a soma de infinitos termos de uma PG de razão 0,01.
Assim:
Sn = a1/1-q
Sn = 0,18/1 - 0,01
Sn = 0,18/0,99
Sn = 18/99 = 2/11
Logo:
3 + 2/11 .:.
(33 + 2)/11
Resposta: 35/11
Acho que é isso, se não for avisem, abraços

JoaoGabriel- Monitor

- Mensagens : 2344
Data de inscrição : 30/09/2010
Idade : 29
Localização : Rio de Janeiro
 Re: Dizima periódica
Re: Dizima periódica
Concordo com o JoaoGabriel, houve um erro na digitação. Concordo também na forma como ele interpretou a dízima (3,18181818181818...). A explicação do nosso amigo está muito elegante, pensei muito se postaria a minha, mas servirá como mais uma alternativa ... se bem que JoaoGabriel foi bem original com essa questão.
É só procurar a fração geratriz da dízima periódica e simplificá-la ao máximo, a partir desse ponto teremos uma fração com os termos primos entre si e então a fração estará irredutível que representa essa dízima -->
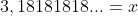
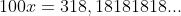
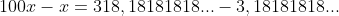
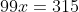
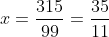
É só procurar a fração geratriz da dízima periódica e simplificá-la ao máximo, a partir desse ponto teremos uma fração com os termos primos entre si e então a fração estará irredutível que representa essa dízima -->

abelardo- Grupo
Velhos amigos do Fórum
- Mensagens : 777
Data de inscrição : 12/03/2011
Idade : 32
Localização : Sertânia, Pernambuco, Brasil
 Re: Dizima periódica
Re: Dizima periódica
Não titubeie para postar, resoluções diferentes são sempre bem vindas!
Eu conhecia este método que você fez, que faz como uma proporção, mas este outro por PG foi mostrado por meu prof. de mat.1 e eu achei bem elegante!
Eu conhecia este método que você fez, que faz como uma proporção, mas este outro por PG foi mostrado por meu prof. de mat.1 e eu achei bem elegante!

JoaoGabriel- Monitor

- Mensagens : 2344
Data de inscrição : 30/09/2010
Idade : 29
Localização : Rio de Janeiro
 matematica
matematica
a resolução esta errada.
Justifique por favor
Justifique por favor
Última edição por JoaoGabriel em Seg 25 Abr 2011, 19:13, editado 1 vez(es) (Motivo da edição : Justificativa by JoaoGabriel)
michael faulstich- Iniciante
- Mensagens : 3
Data de inscrição : 18/04/2011
Idade : 51
Localização : rio de janeiro
 Re: Dizima periódica
Re: Dizima periódica
michael faulstich escreveu:a resolução esta errada
Ok mostre um erro então. Fazendo a divisão na calculadora da exatamente 3,1818181818...
Onde está o erro fera?
PS: Seja mais educado.

JoaoGabriel- Monitor

- Mensagens : 2344
Data de inscrição : 30/09/2010
Idade : 29
Localização : Rio de Janeiro

JoaoGabriel- Monitor

- Mensagens : 2344
Data de inscrição : 30/09/2010
Idade : 29
Localização : Rio de Janeiro
 Re: Dizima periódica
Re: Dizima periódica
a resolução esta errada.
Justifique por favor
Faça a prova REAL!
Porque a Fafa teria digitado o número de forma errada?
Observem que:
3,188181818181...
(318,81818181...)10^-2
(318 + 81/99)10^-2
31563/9900
10521/3300
3507/1100
____________________________________________
"Quando recebemos um ensinamento devemos receber como um valioso presente e não como uma dura tarefa. Eis aqui a diferença que transcende."
Albert Einstein

arimateiab- Elite Jedi

- Mensagens : 776
Data de inscrição : 01/07/2010
Idade : 31
Localização : Estudante de Engenharia de Produção na UFPE.
 Re: Dizima periódica
Re: Dizima periódica
3 x 1881 - 18 / 9900--> 3 1863 / 9900 --> 3 207 / 1100 --> 3507 / 1100
pronto..
e não fui mal educado, só fui sincero
pronto..
e não fui mal educado, só fui sincero
michael faulstich- Iniciante
- Mensagens : 3
Data de inscrição : 18/04/2011
Idade : 51
Localização : rio de janeiro
 Re: Dizima periódica
Re: Dizima periódica
Hola JoaoGabriel.
Pelo simples fato do Michael Faulstich alegar que está errada a questão não significa que o mesmo seja mal educado. Deveríamos agradecê-lo, pois ele está nos alertando que há algo em desacordo e com isso colaborando para que o fórum continue a dar exemplos corretos nas suas soluções.
Seria necessário prestar atenção nessa dízima para perceber onde começa a repetição do período, veja:
3,188181818181
o 3 antes da vírgula é a parte inteira.
O período (é a parte que se repete começa no 81 81 81 ...........
o 18 é a parte não periódica, logo essa dízima é composta, pois o período não começa logo após a vírgula.
No antigo primário era ensinado a escrever a geratriz dessa dízima, assim:
3 + (para numerador a parte não periódica (18), seguida de um dos períodos (81) menos(-) a parte não periódica(18), logo:
3 + (1881 - 18)/
(para denominador tantos noves quantos forem os algarismos do período (81) tem 2 algarismos, então temos 2 noves(99) seguidos de tantos zeros quantos forem os algarismos da parte não periódica (18) tem 2 algarismos, então temos 2 zeros(00), portanto:
3 + (1881 - 18)/(9900)
3 + (1863)/(9900), simplifique a fração toda por 9, fica:
3 + 207/1100, nesse caso temos uma fração mista, basta fazer:
(3*1100 + 207)/1100
(3300 + 207)/1100
3507/1100
Devemos pedir desculpas ao Michael e também a autora da mensagem por terem levantado a dúvida de que a mesma digitou errado a questão.
Pelo simples fato do Michael Faulstich alegar que está errada a questão não significa que o mesmo seja mal educado. Deveríamos agradecê-lo, pois ele está nos alertando que há algo em desacordo e com isso colaborando para que o fórum continue a dar exemplos corretos nas suas soluções.
Seria necessário prestar atenção nessa dízima para perceber onde começa a repetição do período, veja:
3,188181818181
o 3 antes da vírgula é a parte inteira.
O período (é a parte que se repete começa no 81 81 81 ...........
o 18 é a parte não periódica, logo essa dízima é composta, pois o período não começa logo após a vírgula.
No antigo primário era ensinado a escrever a geratriz dessa dízima, assim:
3 + (para numerador a parte não periódica (18), seguida de um dos períodos (81) menos(-) a parte não periódica(18), logo:
3 + (1881 - 18)/
(para denominador tantos noves quantos forem os algarismos do período (81) tem 2 algarismos, então temos 2 noves(99) seguidos de tantos zeros quantos forem os algarismos da parte não periódica (18) tem 2 algarismos, então temos 2 zeros(00), portanto:
3 + (1881 - 18)/(9900)
3 + (1863)/(9900), simplifique a fração toda por 9, fica:
3 + 207/1100, nesse caso temos uma fração mista, basta fazer:
(3*1100 + 207)/1100
(3300 + 207)/1100
3507/1100
Devemos pedir desculpas ao Michael e também a autora da mensagem por terem levantado a dúvida de que a mesma digitou errado a questão.

Paulo Testoni- Membro de Honra

- Mensagens : 3409
Data de inscrição : 19/07/2009
Idade : 77
Localização : Blumenau - Santa Catarina
Página 1 de 2 • 1, 2 
PiR2 :: Matemática :: Álgebra
Página 1 de 2
Permissões neste sub-fórum
Não podes responder a tópicos












