(UNESP)
2 participantes
PiR2 :: Matemática :: Trigonometria
Página 1 de 1
 (UNESP)
(UNESP)
(UNESP) - Dada a equação cos(4x) =
a) Verifique se o ângulo x pertence ao primeiro quadrante, tal que sen(x) =
b) Encontre as soluções da equação dada, em toda a reta.
Gabarito:
a) sim (não entendi esse gabarito...)
b) x =
Obrigada desde já!!!

Carolinethz- Iniciante
- Mensagens : 47
Data de inscrição : 27/09/2015
Idade : 28
Localização : Porto Ferreira, São Paulo, Brasil
 Re: (UNESP)
Re: (UNESP)
Letra A:
No primeiro quadrante sen x>0 e cos x>0. Assim, para sen x=√3/2, calcule cos x utilizando a Relação Fundamental da Trigonometria, sen²x+cos²x=1. Se o valor de cos x encontrado for maior que zero, então, x pertencerá ao primeiro quadrante.
Letra B:
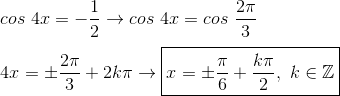
No primeiro quadrante sen x>0 e cos x>0. Assim, para sen x=√3/2, calcule cos x utilizando a Relação Fundamental da Trigonometria, sen²x+cos²x=1. Se o valor de cos x encontrado for maior que zero, então, x pertencerá ao primeiro quadrante.
Letra B:
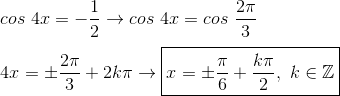
____________________________________________
Charlotte de Witte - Universal Nation

Giovana Martins- Grande Mestre

- Mensagens : 8543
Data de inscrição : 15/05/2015
Idade : 24
Localização : São Paulo
 Re: (UNESP)
Re: (UNESP)
Primeiramente, obrigada pela ajuda!!Giovana Martins escreveu:Letra A:
No primeiro quadrante sen x>0 e cos x>0. Assim, para sen x=√3/2, calcule cos x utilizando a Relação Fundamental da Trigonometria, sen²x+cos²x=1. Se o valor de cos x encontrado for maior que zero, então, x pertencerá ao primeiro quadrante.
Letra B:
De onde exatamente veio o 2k∏?
E eu não consegui fazer a conta do sen²x+cos²x+1 , fiquei um pouco perdida na letra A...

Carolinethz- Iniciante
- Mensagens : 47
Data de inscrição : 27/09/2015
Idade : 28
Localização : Porto Ferreira, São Paulo, Brasil
 Re: (UNESP)
Re: (UNESP)
Disponha!
- O 2k∏ foi utilizado, pois o enunciado não nos forneceu um intervalo, por exemplo, ele não pediu as soluções que estão contidas no intervalo [0,2∏] como é de costume, mas sim apenas as soluções. Lembrando que o 2k∏ representa também todos os arcos côngruos de ± ∏/6 que também são soluções da equação dada.
- Para a letra A:
sen²x+cos²x=1 -> cos²x=1-(√3/2)² ->
cos²x=1/4 -> cos x=√(1/4) -> cos x=1/2
No primeiro quadrante sen x é positivo, assim como cos x também o é. Pelo cálculo acima, cos x=1/2 > 0. Além disso, sen x= √3/2 >0. Portanto, x pertence ao primeiro quadrante.
Se restar dúvidas, avise!
- O 2k∏ foi utilizado, pois o enunciado não nos forneceu um intervalo, por exemplo, ele não pediu as soluções que estão contidas no intervalo [0,2∏] como é de costume, mas sim apenas as soluções. Lembrando que o 2k∏ representa também todos os arcos côngruos de ± ∏/6 que também são soluções da equação dada.
- Para a letra A:
sen²x+cos²x=1 -> cos²x=1-(√3/2)² ->
cos²x=1/4 -> cos x=√(1/4) -> cos x=1/2
No primeiro quadrante sen x é positivo, assim como cos x também o é. Pelo cálculo acima, cos x=1/2 > 0. Além disso, sen x= √3/2 >0. Portanto, x pertence ao primeiro quadrante.
Se restar dúvidas, avise!
____________________________________________
Charlotte de Witte - Universal Nation

Giovana Martins- Grande Mestre

- Mensagens : 8543
Data de inscrição : 15/05/2015
Idade : 24
Localização : São Paulo
 Re: (UNESP)
Re: (UNESP)
Editei minha resposta (em azul).
____________________________________________
Charlotte de Witte - Universal Nation

Giovana Martins- Grande Mestre

- Mensagens : 8543
Data de inscrição : 15/05/2015
Idade : 24
Localização : São Paulo
 Re: (UNESP)
Re: (UNESP)
Giovana Martins escreveu:Letra B:
Agora eu entendi tudinho da letra A, obrigada!!
Mas... olha eu e meu pessimismo em exatas... hahaha
Eu travei a partir do

Carolinethz- Iniciante
- Mensagens : 47
Data de inscrição : 27/09/2015
Idade : 28
Localização : Porto Ferreira, São Paulo, Brasil
 Re: (UNESP)
Re: (UNESP)
Tenha calma, exatas é difícil mesmo  !!
!!
Vamos lá:
4x=±(2∏/3) + 2k∏
Vou tirar o mmc da parte em vermelho (Em todos os passos a seguir, finja que aquele símbolo de mais ou menos nem está ali).
Do mmc: 4x=±(2∏+6k∏)/3
Na parte em azul, eu vou colocar o 2 em evidência
4x=± 2.(∏+3k∏)/3
Simplificando o 4 com o 2:
2x=± (∏+3k∏)/3
Passando o 2 dividindo:
x=± (∏+3k∏)/6
Perceba que há dois termos no numerador, ∏ e 3k∏, cujo denominador de ambos é 6. Daí podemos escrever a fração da seguinte maneira:
x=± (∏/6) + (3k∏/6)
Simplificando o 3 com o 6, x=± (∏/6) + (k∏/2)
Vamos lá:
4x=±(2∏/3) + 2k∏
Vou tirar o mmc da parte em vermelho (Em todos os passos a seguir, finja que aquele símbolo de mais ou menos nem está ali).
Do mmc: 4x=±(2∏+6k∏)/3
Na parte em azul, eu vou colocar o 2 em evidência
4x=± 2.(∏+3k∏)/3
Simplificando o 4 com o 2:
2x=± (∏+3k∏)/3
Passando o 2 dividindo:
x=± (∏+3k∏)/6
Perceba que há dois termos no numerador, ∏ e 3k∏, cujo denominador de ambos é 6. Daí podemos escrever a fração da seguinte maneira:
x=± (∏/6) + (3k∏/6)
Simplificando o 3 com o 6, x=± (∏/6) + (k∏/2)
Última edição por Giovana Martins em Sáb 19 Nov 2016, 21:19, editado 1 vez(es) (Motivo da edição : Eu tinha escrito "cujo o" kkkk)
____________________________________________
Charlotte de Witte - Universal Nation

Giovana Martins- Grande Mestre

- Mensagens : 8543
Data de inscrição : 15/05/2015
Idade : 24
Localização : São Paulo
 Re: (UNESP)
Re: (UNESP)
Giovana Martins escreveu:Tenha calma, exatas é difícil mesmo!!
Vamos lá:
4x=±(2∏/3) + 2k∏
Vou tirar o mmc da parte em vermelho (Em todos os passos a seguir, finja que aquele símbolo de mais ou menos nem está ali).
Do mmc: 4x=±(2∏+6k∏)/3
Na parte em azul, eu vou colocar o 2 em evidência
4x=± 2.(∏+3k∏)/3
Simplificando o 4 com o 2:
2x=± (∏+3k∏)/3
Passando o 2 dividindo:
x=± (∏+3k∏)/6
Perceba que há dois termos no numerador, ∏ e 3k∏, cujo o denominador de ambos é 6. Daí podemos escrever a fração da seguinte maneira:
x=± (∏/6) + (3k∏/6)
Simplificando o 3 com o 6, x=± (∏/6) + (k∏/2)
Nossa, agora ficou tudo lindo e explicadinho.
Muito obrigada mesmo pela atenção, você é um anjo!


Carolinethz- Iniciante
- Mensagens : 47
Data de inscrição : 27/09/2015
Idade : 28
Localização : Porto Ferreira, São Paulo, Brasil
 Re: (UNESP)
Re: (UNESP)
De nada!!


____________________________________________
Charlotte de Witte - Universal Nation

Giovana Martins- Grande Mestre

- Mensagens : 8543
Data de inscrição : 15/05/2015
Idade : 24
Localização : São Paulo
PiR2 :: Matemática :: Trigonometria
Página 1 de 1
Permissões neste sub-fórum
Não podes responder a tópicos












