Federal Goiás.
2 participantes
PiR2 :: Matemática :: Álgebra
Página 1 de 1
Federal Goiás.
por mari Qui 18 Fev 2016, 14:16
Considere a equação 
, onde m é um número real.
a)Para m=-1, determine a raíz real da equação.
b)Determine os conjuntos de valores de m, para os quais a equação possui uma raíz real
a)
x+√x²+x+(-1)=-1
√x²+x-1=-1-x
x²+x-1=(-1-x)²
x²+x-1=1+2x+x²
x-1=1+2x
-2=x
Alguém sabe a b?
, onde m é um número real.a)Para m=-1, determine a raíz real da equação.
b)Determine os conjuntos de valores de m, para os quais a equação possui uma raíz real
a)
x+√x²+x+(-1)=-1
√x²+x-1=-1-x
x²+x-1=(-1-x)²
x²+x-1=1+2x+x²
x-1=1+2x
-2=x
Alguém sabe a b?
- gabarito:
mari- Estrela Dourada
- Mensagens : 1134
Data de inscrição : 01/09/2015
Idade : 26
Localização : São Paulo
Re: Federal Goiás.
por Cleyton Qui 18 Fev 2016, 21:26
Olá 
Pensando na extração da raiz, podemos fazer:
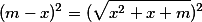
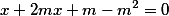
Com isso, chegamos na seguinte equação do 2° grau:
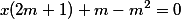
Para que a equação possua uma única raiz real, devemos ter
. Logo,
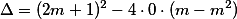
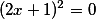
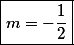
Pensando na extração da raiz, podemos fazer:
Com isso, chegamos na seguinte equação do 2° grau:
Para que a equação possua uma única raiz real, devemos ter
. Logo,
Cleyton- Jedi
- Mensagens : 228
Data de inscrição : 14/08/2009
Localização : Minas Gerais
mari- Estrela Dourada
- Mensagens : 1134
Data de inscrição : 01/09/2015
Idade : 26
Localização : São Paulo
Tópicos semelhantes» Federal Uberlândia
» U Católica Goiás - Lançamento Oblíquo
» Olimpiada de Matemática do Estado de Goiás (Modificada)
» (Federal de Viçosa) - Conjuntos
» Federal Ceará
» U Católica Goiás - Lançamento Oblíquo
» Olimpiada de Matemática do Estado de Goiás (Modificada)
» (Federal de Viçosa) - Conjuntos
» Federal Ceará
PiR2 :: Matemática :: Álgebra
Página 1 de 1
Permissões neste sub-fórum
Não podes responder a tópicos
