Circunferência inscrita no triângulo

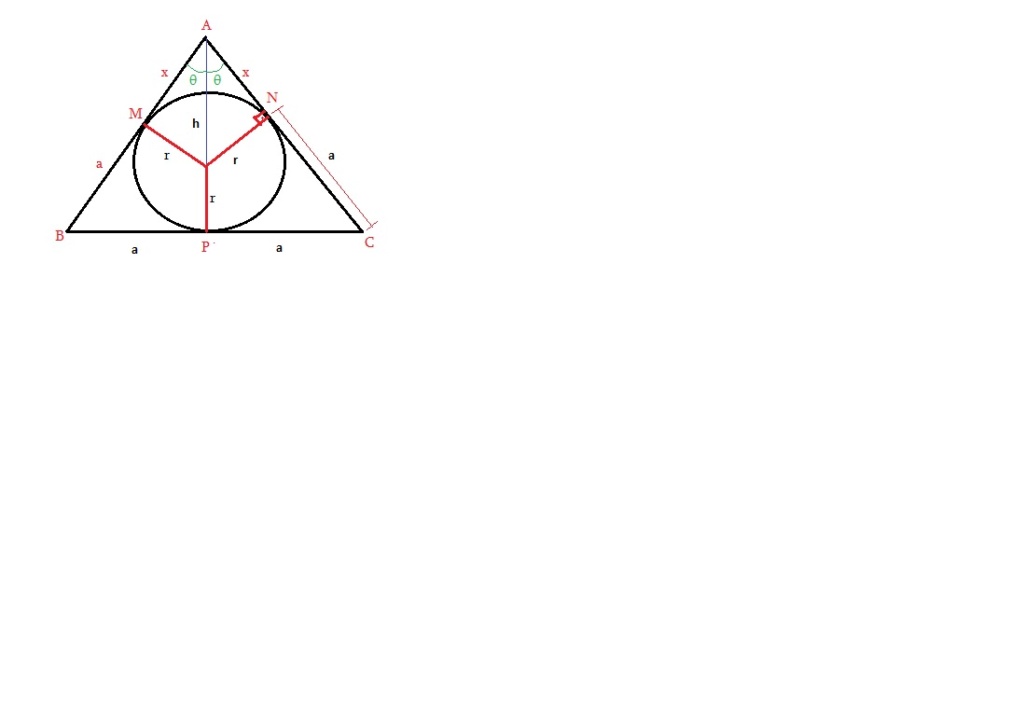
Num triângulo isósceles ABC com AB = AC, tem-se BC = 2a e o raio da circunferência inscrita é r (a > r). Calcule, em função de a e r:

[img]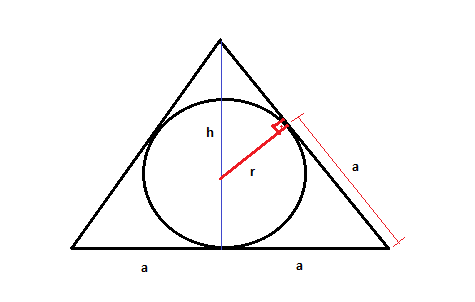[/img]

a) a medida do lado AB do triângulo.

b) a medida da altura relativa à base.

A no alto, B à esquerda, C à direita e O o centro da circunferência
Sejam M, N os pontos de tangência da circunferência com AB e AC
Seja M o ponto médio de BC (BM = CM = a) e AM = AN = x

BM = BP = CN = CP = a ---> OM = ON = OP = r ---> OA = h

h² = r² + x² ---> AP = AO + OP ---> AP = h + r

ON/AN  = CP/AP ---> r/x = a/(h + r) ---> r.(h + r) = a.x ---> r.h + r² = a.x --->

r.h = a.x - r² ---> r².h² = (a.x - r²)² ---> r².(r² + x²) = a².x² - 2.a.r².x + (r²)² 

r².x² = a².x² - 2.a.r².x ---> x².(a² - r²) - 2.a.r².x = 0 ---> x.[x.(a² - r²) - 2.a.r²] = 0

x = 0 (não serve) ---> x.(a² - r²) - 2.a.r² = 0 ---> x = 2.a.r²/(a² - r²)

AB = AM + BM ---> AM = x + a ---> AB = 2.a.r²/(a² - r²) + a ---> 

AB = a.(a² + r²)/(a² - r²)

Por favor confira as contas

Complete, por favor, calculando o que se pede.

Mestre, poderia me explicar alguns passos da sua resolução ?
Primeiramente, por que iremos considerar que BM e CN valem a ? Se M e N são pontos médios de AB e AC, respectivamente, sendo AM = AN = x, então BM e CN também deveriam ser x, não ?

E como o senhor fez aquela semelhança ? ON/AN = CP/AP. Pra mim, não faz sentido...

PS: na questão original não se dá a figura, apenas o enunciado. A figura e tudo o mais devem ser feitos por quem irá resolver a questão.

Eu escrevi errado que M e N são pontos médios de AB e AC
M e N são pontos de tangência da circunferência com AB e AC. Já editei.

ABC é isósceles (AB = AC) --> Logo, BP = CP ---> P é o pé da altura AP

Os triângulos ANO e APC tem o mesmo ângulo θ, logo:

tgθ = ON/AN = CP/AP

Ahhh, perfeito, Mestre. Agora entendi a semelhança.
Quanto ao fato de BM e CN valerem a, a gente teria enxergar que os triângulos BPM e CNP também são isósceles ? Tipo, na base da visualização mesmo, ou há outra maneira de enxergar BM = CN = a ?

BM = BP = a e CN = CP = a porque são tangentes à circunferência pelo mesmos pontos externos, B e C

Perfeitíssimo!!!!!!!
Sem mais perguntas.
Obrigado, Mestre.

tem gabarito ?

Raimundo, é a resposta do Mestre Élcio.
AB = a.(a² + r²)/(a² - r²)