PG e exponencial

(Ufu 2012) Os “fractais” são criados a partir de funções matemáticas cujos cálculos são transformados em imagens. Geometricamente, criam-se fractais fazendo-se divisões sucessivas de uma figura em partes semelhantes à figura inicial. Abaixo destacamos o Triângulo de Sierpinski, obtido através do seguinte processo recursivo: 



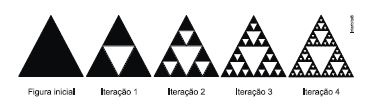
— Considere um triângulo equilátero de 2 1cm de área, conforme a Figura Inicial. Na primeira iteração, divida-o em quatro triângulos equiláteros idênticos e retire o triângulo central, conforme figura da Iteração 1 (note que os três triângulos restantes em preto na Iteração 1 são semelhantes ao triângulo inicial). 
— Na segunda iteração, repita o processo em cada um dos três triângulos pretos restantes da primeira iteração. E assim por diante para as demais iterações. Seguindo esse processo indefinidamente, obtemos o chamado Triângulo de Sierpinski. 

Considerando um triângulo preto em cada iteração, da iteração 1 até a iteração N, e sabendo que o produto dos valores numéricos das áreas desses triângulos é igual a 1/2^240 então N é:
a) é um número primo.
b) é múltiplo de 2.
c) é um quadrado perfeito.
d) é divisível por 3.

Resposta: letra D.

Vi algumas resoluções em outros sites e eles resolveram da seguinte forma: (1/4)^n . (1/4)^n(n-1)/2 = 1/2^240
Entendi que a razão é 1/4, mas não entendi porque elevaram 1/4 a n(n-1)/2. Alguém poderia me explicar ou me ajudar a resolver de alguma outra forma?? 
Obrigada desde já.

Note que cada triângulo preto novo terá metade da altura e metade da base do que lhe deu origem, portanto cada nova área é 1/4 da anterior.

O produto das áreas é:
P = 2^-240

A PG das áreas é tal que:
a₁ = 1/4 = 2^-2
a_n = 2^-2*(1/4)^n-1 = 2^-2n
a₁*a_n = 2^-2(n+1)

Portanto,
P² = (a₁*a_n)ⁿ ---->  2^2*(-240) = 2^-2(n²+n) -----> 2²⁴⁰ = 2^(n²+n)

Igualando os expoentes, obtemos:
240 = n² + n
n = 15

Sobre a sua dúvida, eleveram a n(n-1)/2 porque quando multiplicamos uma PG, aparece uma soma de expoentes na razão:
a, aq, aq², aq³, ..., aqⁿ
Multiplicando tudo:
P = aⁿ⁺¹ * q^{(1 + 2 + ... + n)} = aⁿ⁺¹ * q^n(n-1)/2
Note que aparece a soma da PA na razão e é daí que veio. Na minha solução não apareceu porque eu uso uma outra equação para o produto (não tão convencional), que é a exposta ali: P² = (a₁*a_n)ⁿ.

Perfeito! Valeu por esclarecer a dúvida. Não tinha prestado atenção na multiplicação das PGs. 
Só uma observação: estava olhando a questão original e percebi que o primeiro termo da PG das áreas é 1/4. Talvez você tenha colocado a1=2 devido ao meu erro de digitação: "Considere um triângulo equilátero de 2 1cm de área" sendo que o correto seria "Considere um triângulo equilátero de 1 cm² de área". Dai nesse caso a equação de 2º grau ficaria assim: n²+n-240=0. Logo, n=15, que é divisível por 3 (alternativa d). 
Perdão pelo erro! E obrigada mais uma vez.

Pois é, Angélica, fiquei em dúvida sobre quem era o primeiro termo exatamente. Que coincidência ter dado uma das respostas possíveis. Mas já arrumei a solução. Disponha!

Ok! Sim sim, coincidência mesmo. Eles colocam alternativas com possíveis resultados para que, propositalmente, nos induza a errar a questão   kkkk