valores extremos
2 participantes
Página 1 de 1
valores extremos
por luiz Sex 28 maio 2010, 09:35
4-Para quaisquer valores a e b, mostre que:
(a)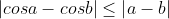
(b)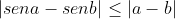
(a)
(b)
luiz- Iniciante
- Mensagens : 33
Data de inscrição : 24/05/2010
Idade : 49
Localização : beberibe-ce
Re: valores extremos
por aryleudo Dom 30 maio 2010, 20:19
ITEM A
|cos(a) - cos(b)|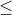
|a - b|
SOLUÇÃO
Sabemos que: |cos(x)|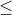 1
Considere f(x) = cos(x). Daí, f'(x) = -sen(x), como estamos fazendo uso do módulo,
|f'(x)| = |-sen(x)| = |sen(x)|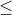 1.
Existe pelo menos um c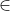
(a, b) tal que
%20=%20\frac{f(b)%20-%20f(a)}{(b-a)})
| = |sen(c)| \leq 1\Rightarrow f%27(c)%20=%20\frac{f(b)%20-%20f(a)}{(b-a)} \leq 1 \Rightarrow \left |\frac{cos(b)-cos(a)}{(b-a)} \right | \leq 1)
OBS1.: Temos que
 - cos(a)|}{|b - a|} \leq 1 \Rightarrow |cos(b) - cos(a)| \leq |b - a|)
OBS2.: Note que |x - y| = |y - x|
 - cos(a)| \leq |a - b|)
.
|cos(a) - cos(b)|
SOLUÇÃO
Sabemos que: |cos(x)|
Considere f(x) = cos(x). Daí, f'(x) = -sen(x), como estamos fazendo uso do módulo,
|f'(x)| = |-sen(x)| = |sen(x)|
Existe pelo menos um c
OBS1.: Temos que
OBS2.: Note que |x - y| = |y - x|
____________________________________________
"Há três coisas na vida que não voltam: As palavras, o tempo e as oportunidades."
Autor Desconhecido
aryleudo- Grande Mestre
- Mensagens : 2292
Data de inscrição : 01/10/2009
Idade : 41
Localização : Cascavel/CE - Brasil
Re: valores extremos
por aryleudo Dom 30 maio 2010, 20:33
ITEM B
|sen(a) - sen(b)|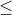 |a - b|
SOLUÇÃO
Considere f(x) = sen(x). Daí, f'(x) = cos(x), como estamos fazendo uso do módulo,
|f'(x)| = |cos(x)|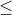 1.
Existe pelo menos um c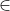
(a, b) tal que  = \frac{f(b) - f(a)}{(b - a)})
 = |cos(c)| \leq 1 \Rightarrow \left |\frac{f(b) - f(a)}{(b - a)} \right | \leq 1 \left |\frac{sen(b) - sen(a)}{(b - a)} \right | \leq 1)
OBS1.: Temos que
-sen(a)|}{|b - a|} \leq 1 \Rightarrow |sen(b)-sen(a)| \leq |b - a|)
OBS2.: Note que |x - y| = |y - x|
-sen(a)| \leq |a - b|)
|sen(a) - sen(b)|
SOLUÇÃO
Considere f(x) = sen(x). Daí, f'(x) = cos(x), como estamos fazendo uso do módulo,
|f'(x)| = |cos(x)|
Existe pelo menos um c
OBS1.: Temos que
OBS2.: Note que |x - y| = |y - x|
____________________________________________
"Há três coisas na vida que não voltam: As palavras, o tempo e as oportunidades."
Autor Desconhecido
aryleudo- Grande Mestre
- Mensagens : 2292
Data de inscrição : 01/10/2009
Idade : 41
Localização : Cascavel/CE - Brasil
Tópicos semelhantes» valores extremos
» valores extremos
» valores extremos na circunferência
» Extremos locais da função
» Extremos absolutos
» valores extremos
» valores extremos na circunferência
» Extremos locais da função
» Extremos absolutos
Página 1 de 1
Permissões neste sub-fórum
Não podes responder a tópicos
