Retas Paralelas cortada por Transversal

Olá Alon3Wol4. Tem uma regra que diz que a questão deve ser digitada, mas questões de geometria quase não tem enunciado.


Então, para questões de retas paralelas que aparecem esse "bico" no meio das paralelas o segredo é simplesmente traçar outra paralela, vou resolver o item da esquerda, provavelmente você conseguirá resolver o da direita em seguida. Veja:

1- Onde há "bico" tracei t, sendo t paralela a r e s.



2- 20º desenhado por ser opostos pelo vértice.




3- Como t é paralela a s, encontramos aquele 20º da figura, e fazendo analogamente para 60º de cima, encontramos o valor de x como 20º+60º = 80º

O caso da letra B é análogo.


Qualquer dúvida avise.

 Por nada.

Vamos generalizar:


Sejam as retas k e l, paralelas, é verdade que x=α+β

Demonstração



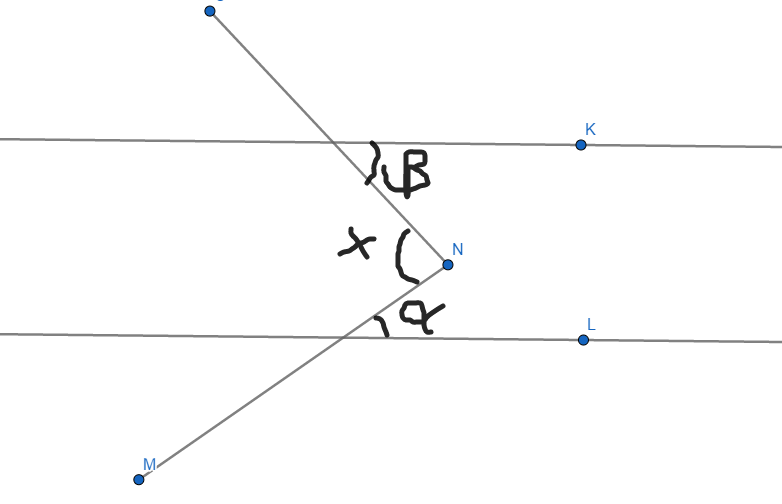
Seja m, uma terceira reta, paralela as retas k e l, traçada pelo "bico":








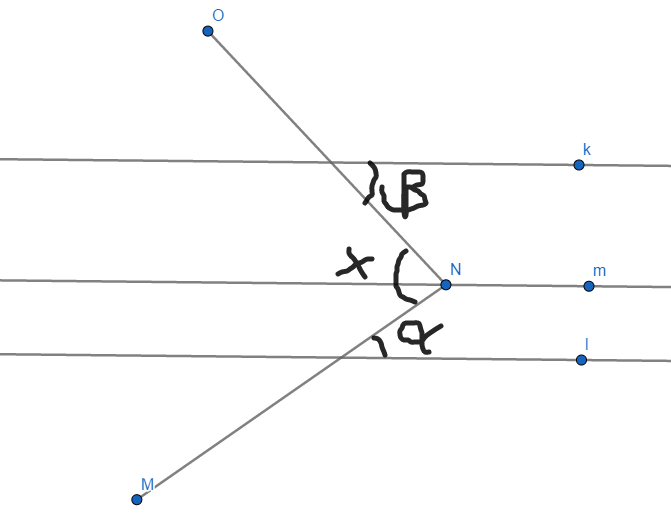
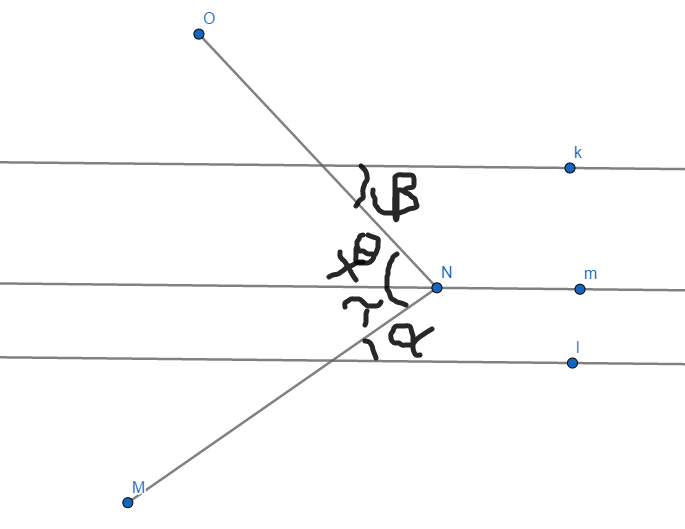
Como m//l, α e γ são alternas internos, implicando que α=γ (I)

Analogamente, β=θ.  (II)

Como x=θ+γ,  de (I) e (II), x= α+β  



CQD.

Como aprofundamento, deixo com você um video para casos que aparecem n "bicos", conhecido como teorema dos bicos, demonstrado de uma maneira intuitiva pelo professor Paulo no  canal da OBMEP.

https://www.youtube.com/watch?v=wvcsKakDVVc