Teorema dos feixes harmônicos

Mostre que um feixe harmônico determina em uma secante qualquer, quatro pontos de divisão harmônica. 







Demonstração do livro:



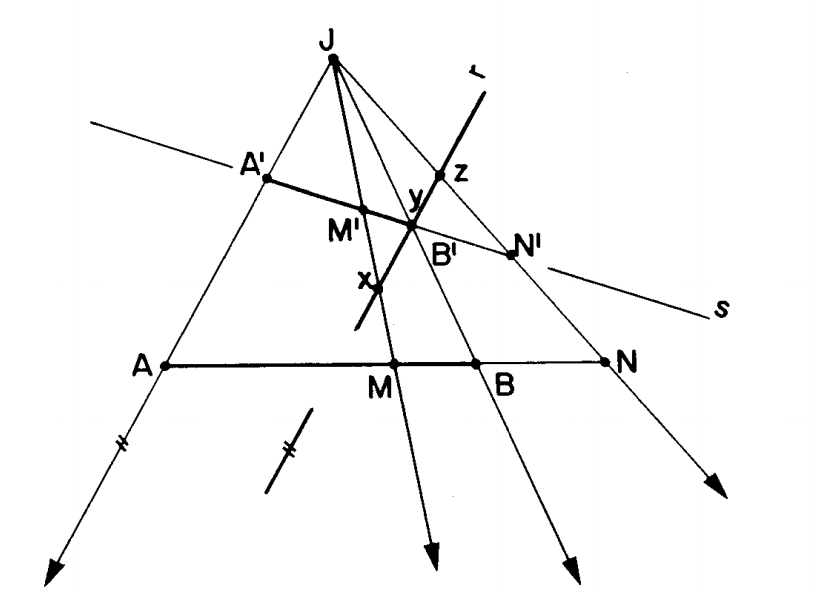
Seja J(AMBN) um feixe harmônico e uma secante s que determina os pontos A', M', B' e N'. Ora, se r//JA' determina xy=yz (pois J-AMBN é feixe harmônico), então J(A'M'B'N') é um feixe harmônico, sendo M' e N' conjugados harmônicos de A'B'.


Eu só não entendi porque o fato de xy=yz faz com que o feixe J(A'M'B'N') seja harmônico.

Normalmente eu nao conseguiria resolver, mas me bateu uma inspiraçao rsrs'

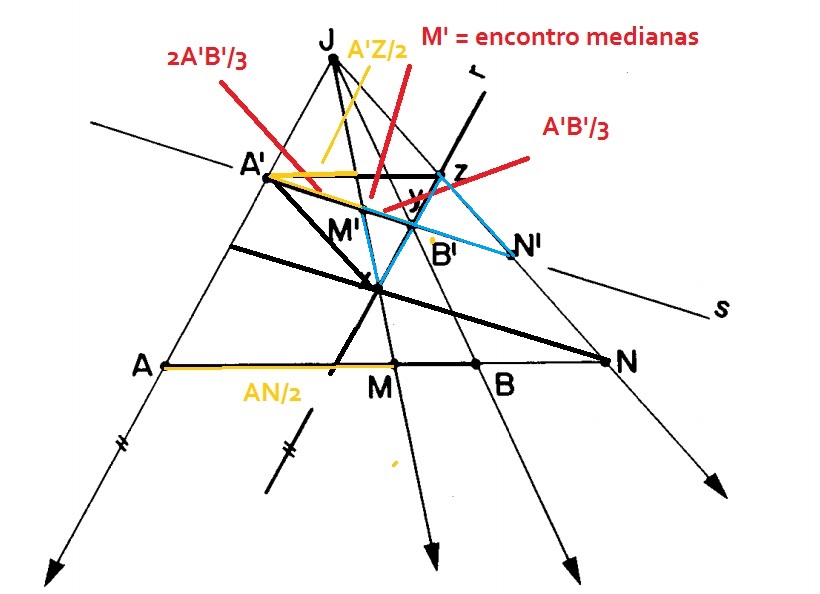
Veja que, se eu tenho uma mediana (xy e yz sao iguais, indicando em A'y uma mediana) e um ponto de encontro em as medianas, eu tenho essa relaçao de divisao na mediana: 2M/3 e M/3, somando daria 3M/3 = M, isso eh algo conceitual tirado da teoria das cevianas


Eu quero provar que a relaçao A'J'(ponto na extremidade da linha em amarelo) e J''Z eh igual a relaçao entre A'M' e M'N', entao tenho que pensar em focar em A'J' = A'Z/2

Como A'J' eh a divisao oriunda de uma das medianas, essa relaçao A'J' e J'Z eh igual a 1, assim como A'M' e M'N" - porque se voce perceber, os triangulos em azul sao semelhantes (semelhança LAL), por ser LAL, yN' = M'y = M/3, e M/3+ M/3 = M'N' = A'M' = 2M/3. 


Portanto a relaçao ficaria A'M'/M'N' = A'J'/J'Z = 1

Nickds12 escreveu:Normalmente eu nao conseguiria resolver, mas me bateu uma inspiraçao rsrs'

Veja que, se eu tenho uma mediana (xy e yz sao iguais, indicando em A'y uma mediana) e um ponto de encontro em as medianas, eu tenho essa relaçao de divisao na mediana: 2M/3 e M/3, somando daria 3M/3 = M, isso eh algo conceitual tirado da teoria das cevianas


Eu quero provar que a relaçao A'J'(ponto na extremidade da linha em amarelo) e J''Z eh igual a relaçao entre A'M' e M'N', entao tenho que pensar em focar em A'J' = A'Z/2

Como A'J' eh a divisao oriunda de uma das medianas, essa relaçao A'J' e J'Z eh igual a 1, assim como A'M' e M'N" - porque se voce perceber, os triangulos em azul sao semelhantes (semelhança LAL), por ser LAL, yN' = M'y = M/3, e M/3+ M/3 = M'N' = A'M' = 2M/3. 


Portanto a relaçao ficaria A'M'/M'N' = A'J'/J'Z = 1

Tinha até esquecido desse post. Mais tarde vou dar uma olhada com calma. Obrigado pela ajuda!