Perpendicularidade

Demonstre que: " Se dois angulos nao complanares tem os lados paralelos e sao de especie diferente, aqueles angulos sao suplementares( Dica: Prolongue um dos lados de um dos angulos).

O primeiro passo é perceber que ângulos formados pelos lados, podem ser vistos como ângulos formados pelas retas que contêm os lados (que é justamente a dica de prolongar um lado). Veja:



Note ainda que duas retas concorrentes sempre apresentam dois ângulos diferentes (β e o seu suplementar).
O segundo passo é usar que, como os dois ângulos pertencem à planos diferentes, além de terem os lados paralelos (e com isso, retas paralelas), pela definição de planos paralelos: "dois planos são paralelos se duas retas concorrentes de um são paralelas às do outro", concluímos que os planos dos ângulos são paralelos.
Agora fica mais fácil de ver que as retas formam os mesmos ângulos. Veja:



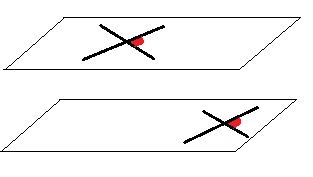
Se quiser provar isso mais formalmente, basta projetar as retas de um plano no outro (mantendo, assim, o ângulo entre as retas), e dizer que "arrastar" retas concorrentes paralelamente não altera o ângulo entre elas. 
Com isso, concluímos que as retas que contém os lados dos dois ângulos em questão formam os mesmos ângulos. Como os ângulos em questão são diferentes, temos que estes são suplementares (um dos lados já está desenhado na figura 1, tendo um ângulo β, o outro teria o ângulo em azul, que é 180^o-β).