Como determinar o domínio da função logcos(x)

por Caique Souza Qui 15 Fev 2018, 00:41

Boa noite.

Determine o domínio da seguinte função log cos(x).

A minha resposta foi: Dom: {x e R / 3pi/2+2kpi < x < pi/2+2kpi}, mas a resposta verdadeira é [-pi/2+2kpi, pi/2+2kpi].

Não entendi.. Por que -pi/2? Por que errei?

Grato pela ajuda.

por **Euclides** Qui 15 Fev 2018, 01:25

Sua resposta deveria ter sido:

$\\\log a\;\to\;a>0\;\;\therefore \;\;\cos x>0\\\\\frac{3\pi}{2}+2k\pi<x<2\pi+2k\pi\;\;e\;\;0+2k\pi<x<\frac{\pi}{2}+2kpi$

que equivale à resposta correta.

Como determinar o domínio da função logcos(x) Fig_2

Como determinar o domínio da função logcos(x) Fig_2

por Caique Souza Qui 15 Fev 2018, 12:40

Muito obrigado Euclides!

Percebi que a resposta tem que ser dada desse jeito, porque, no caso, cos x tem que também ser diferente de 1, devido às propriedades do log.

Este site é um excelente projeto. Abs.

por **Elcioschin** Qui 15 Fev 2018, 21:45

Não Caique

As restrições de logaritmos são:

1) Base > 0 e base ≠ 1 ---> Nesta questão não se aplica, por que, em log(cosx) a base é 10

2) Logaritmando > 0 ---> nesta questão: cosx > 0 --->

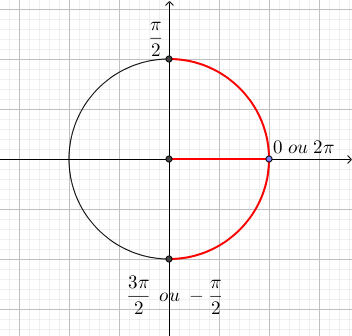
2.1) cos x = 0, para x = pi/2 ou x = 3.pi/2 (na 1ª volta)
2.2) cosx < 0, no intervalo pi/2 < x < 3.pi/2 (na 1ª volta)

Logo, na 1ª volta, são válidos todos os ângulos nos intervalos 0 ≤ x < pi/2 e 3.pi/2 < x ≤ 2.pi

Explicando melhor: Na 1ª volta, para x = 0 ou x = 2.pi ---> cosx = 1 ---> log(cosx) = log1 = 0 ---> Faz parte do domínio

por Caique Souza Sex 16 Fev 2018, 00:54

Ah, okay.

E a resposta só fica em duas partes 0 ≤ x < pi/2 e 3.pi/2 < x ≤ 2.pi devido ao fato de os intervalos não serem em quadrantes consecutivos?

Se o intervalo fosse compreendesse os quadrantes I e II, não precisaríamos da conjunção "e", certo? Acho que isso que me confundiu..

Abs.

por **Elcioschin** Sex 16 Fev 2018, 22:02

A soluções ficam em quadrantes consecutivos sim: 4º e 1º:

O 4º quadrante vai de 3.pi/2 (270º) a 2.pi (360º) e o 1º quadrante vai de 0 a pi/2 (90º) (que é o mesmo de 360º a 450º)

Neste caso deve-se separar em dois intervalos.