Valores máximos e mínimos (derivada)

por Felipenrc Sáb 01 Jul 2017, 19:18

Por gentileza, gostaria de ajuda nessa questão:
Um cone é feito de uma folha circula com raio R recortando um setor e colando os lados que sobraram. Qual o ângulo do setor circular recortado para obtermos um cone com volume máximo, sabendo que a área lateral de um cono de raio r e altura h é:
A= π.r.²√(r²+h²) .
Obs: o r² + h² estão dentro de uma raiz quadrada.
Agradeço a disponibilidade.

por **LPavaNNN** Sáb 15 Jul 2017, 13:19

a geratriz do cone é o R :

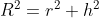
$R^2=r^2+h^2$

o comprimento da circunferência da base do cone, é o comprimento do setor usado na sua formação, sendo theta= ângulo do setor retirado:

$(2\pi- \theta)R=2\pi r\\r^2=\frac{(4\pi^2-4\pi \theta+\theta^2)R^2}{4\pi^2}\\\text{usando esse resultado na primeira equacao:}\\h^2=\frac{R^2(4\pi^2-4\pi^2+4\pi\theta-\theta ^2)}{4\pi^2}\\h=\frac{R\sqrt{4\pi \theta-\theta^2}}{2\pi}\\V=\frac{\pi r^2h}{3}=\frac{\pi}{3}.(4\pi^2-4\pi\theta+\theta^2).\frac{R^2}{4\pi^2}.\frac{R\sqrt{4\pi \theta-\theta^2}}{2\pi}=\frac{R^3}{24\pi^2}(4\pi^2-4\pi \theta+\theta^2).\sqrt{4\pi \theta-\theta^2}\\\frac{dV}{d\theta}=\frac{R^3}{24\pi^2}((-4\pi+2\theta)\sqrt{4\pi \theta-\theta^2}+(4\pi^2-4\pi \theta+\theta^2)\frac{4\pi-2\theta}{2\sqrt{4\pi\theta-\theta^2}})\\\frac{dv}{d\theta}=0\\(4\pi-2\theta)(\frac{4\pi^2-4\pi \theta+ \theta ^2}{2\sqrt{4\pi \theta-\theta^2}}-\sqrt{4\pi\theta-\theta^2})=0$

como thet diferente de 2pi, então:

$\frac{4\pi^2-4\pi \theta+ \theta ^2}{2\sqrt{4\pi \theta-\theta^2}}-\sqrt{4\pi\theta-\theta^2}=0\\4\pi^2-4\pi\theta+\theta^2-2(4\pi\theta-\theta^2)=0\\3\theta^2-12\pi\theta+4\pi^2=0\\\Delta=144\pi^2-48\pi^2\\\theta=\frac{12\pi\pm \sqrt{96\pi^2}}{6}\\\theta=\frac{12\pi\pm 4\pi\sqrt{6}}{6}$

basta saber qual é o ponto de máximo, partindo de dv/dTheta,

procurando saber onde ela é crescente:

$\frac{R^3}{24\pi^2}(-4\pi+2\theta)(\sqrt{4\pi\theta-\theta^2}-(\frac{4\pi^2-4\pi\theta+\theta^2}{2\sqrt{4\pi\theta-\theta^2}}))>0\\-4\pi+2\theta<0\\\frac{R^3}{24\pi^2}>0\\\sqrt{4\pi\theta-\theta^2}-(\frac{4\pi^2-4\pi\theta+\theta^2}{2\sqrt{4\pi\theta-\theta^2}})<0\\8\pi\theta-3\theta^2-4\pi^2+4\pi\theta < 0\\3\theta^2-12\pi\theta+4\pi^2>0\\\text{ou seja a funcao e crescente para }\theta<x_1 \text{ou }\theta>x_2\\pois \frac{dv}{d\theta}>0,se \ \ \theta < x_1 \ \ ou \ \ \theta>x_2$

ou seja, o volume é maior quando :

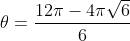
$\theta=\frac{12\pi-4\pi\sqrt6}{6}$