(UESPI) Razão de semelhança
2 participantes
Página 1 de 1
(UESPI) Razão de semelhança
por shady17 Seg 1 Ago 2016 - 13:28
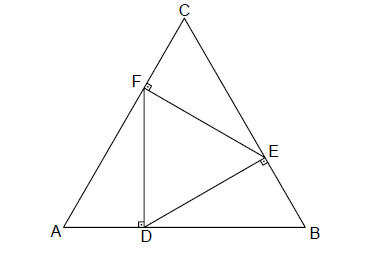
Na ilustração abaixo, os triângulos ABC e DEF são equiláteros e os lados DE, EF e FD são perpendiculares, respectivamente, aos lados BC, CA e AB. Qual a razão entre as áreas de ABC e DEF?
- Spoiler:
- 3,0
shady17- Jedi
- Mensagens : 322
Data de inscrição : 23/05/2013
Idade : 33
Localização : Uberlândia MG
Re: (UESPI) Razão de semelhança
por Claudir Seg 1 Ago 2016 - 15:50
y.cos30 = l
y.sen30 = x
y + x = L
L/l = (y+y.sen30)/y.cos30 = √3
S/s = (L/l)² = 3
* A razão entre as áreas é igual ao quadrado da razão de semelhança.
____________________________________________
"Death is so terribly final, while life is full of possibilities." - Tyrion Lannister
Claudir- Monitor
- Mensagens : 1938
Data de inscrição : 13/04/2014
Idade : 28
Localização : Gravataí - RS -
shady17- Jedi
- Mensagens : 322
Data de inscrição : 23/05/2013
Idade : 33
Localização : Uberlândia MG
Tópicos semelhantes» Razão de semelhança
» Razão de semelhança
» Razão de Semelhança
» Razão de Semelhança
» Razão de semelhança
» Razão de semelhança
» Razão de Semelhança
» Razão de Semelhança
» Razão de semelhança
Página 1 de 1
Permissões neste sub-fórum
Não podes responder a tópicos
