Por: Euclides

Nasceu (287 aC) e viveu em Siracusa de onde se ausentou pelo período em que viveu em Alexandria e travou conhecimento com os sábios da Biblioteca. Foi morto aos 75 anos por um soldado das legiões de Marcelo que tomaram Siracusa. Sobre essa morte há algumas versões, muito parecidas, de que, concentrado em um problema geométrico, não fez caso da presença do soldado romano que lhe ordenava que o acompanhasse e, enfurecido com o desdém do sábio, matou-o.

Entre suas inúmeras invenções e descobertas científicas a compreensão da natureza do Empuxo hidrostático é um de seus trabalhos mais conhecidos.

Embora Arquimedes tivesse descoberto o trato físico e matemático do empuxo quase 2.000 anos antes de Newton, essa é uma força de natureza newtoniana que obedece à segunda lei.


Causas mecânicas do empuxo

Esta é uma abordagem que pode ser feita 2.000 anos depois, após os trabalhos de Baise Pascal (1623-1662), Simon Stevin (1548-1629) e Isaac Newton (1642-1727).

Considere o cilindro submerso representado na figura abaixo: 

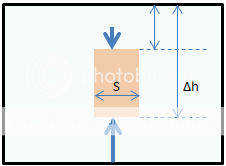
Devido ao gradiente de pressão, a força aplicada na base do cilindro será maior que a força aplicada na tampa superior. A força resultante para cima é o Empuxo.



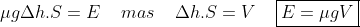
resultando que o empuxo de Arquimedes é uma força igual ao peso da massa de água deslocada.

Se o empuxo for maior que o peso do corpo, a resultante é vertical e para cima e o corpo flutua, se menor, a resultante é para baixo e o corpo desce ao fundo. Nos dois casos a aceleração é tal como enunciada por Newton. Em igualdade de intensidades o corpo apresenta equilíbrio indiferente em qualquer posição vertical de imersão total.

Da expressão do empuxo verifica-se que, dado um corpo com volume e densidade definidos, o agente que quantifica o empuxo é a aceleração da gravidade. De outra maneira, a aceleração é o agente causador do gradiente de pressão que origina o empuxo. Isto explica-se pelo fato de que, a cada profundidade, a pressão é resultado do peso da coluna de água acima. Podemos dizer que o líquido vai sendo "compactado" pelo próprio peso.

Considere agora a figura abaixo, que representa uma bolinha de ping-pong de massa desprezível, submersa e presa ao fundo do recipiente por um fio.

se o recipiente for agora acelerado uniformemente para a direita, como se comportará a bolinha?

a) permanece na vertical?
b) inclina-se para a esquerda?
c) inclina-se para a direita?

qualquer aceleração será capaz de produzir um gradiente de pressão

Resolução:

a aceleração horizontal para a direita produz um gradiente de pressão já que o líquido recebe uma força de natureza inercial para a esquerda. Haverá, portanto, um empuxo horizontal para a direita. Pelo princípio da independência da ação das forças, a bolinha estará sujeita a um empuxo vertical para cima e um empuxo horizontal para a direita, cuja resultante será perpendicular à interface do líquido, fazendo a bolinha inclinar-se para a direita.

Pela mesma razão, a tensão no fio na segunda situação será maior que a tensão no repouso. Teremos





Um outro exemplo:

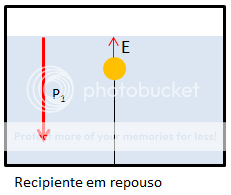
Um corpo sólido está em equilíbrio mergulhado em um líquido cuja densidade é maior que a densidade do corpo que está preso ao fundo do recipiente por um fio. A tensão no fio é T₁ quando o recipiente está em repouso . Mostre que a tensão T , quando o recipiente tem uma aceleração vertical para cima a,é dada por T₁(1+a/g)

Resolução:

Vamos resolvê-la agora equacionando uma condição estática no referencial não-inercial do recipiente em movimento.

Quando o sistema está em repouso temos uma situação simples em que:



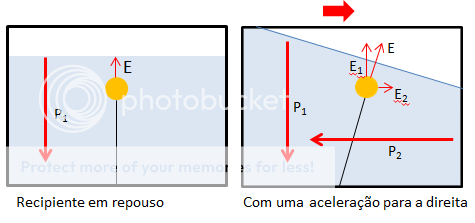
No segundo momento temos um referencial acelerado (à semelhança de um elevador) em que o corpo apresenta um peso aparente e um novo empuxo composto pelo empuxo de Arquimedes e o empuxo de Newton (devido à aceleração), sendo

 (*)


No ponto de vista do referencial não inercial temos outra situação de equilíbrio



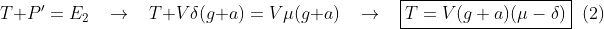
relacionando ambas as expressões:




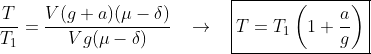
(*) Consulta - aceleração nos elevadores

      Forças e acelerações nos elevadores