Algebra Linear - transformação de rotação.

Me ajude com essa questão.

Os pontos A(2, – 1) e B(– 1, 4) são vértices consecutivos de um quadrado. Calcule os outros dois vértices, utilizando a transformação de rotação. 
Escolha uma:

a. (– 3, 2) e (4, –  ou (5, – 1) e (– 2, – 6)
b. (3, 6) e (5, 1) ou (– 5, 2) e (– 4, – 3)
c. (4, 7) e (7, 2) ou (– 6, 1) e (– 3, – 4)
d. (5, 9) e (9, 1) ou (– 9, – 5) e (– 5, – 9)
e. (4, – 8)e (– 8, 3) ou (– 7, 2) e (– 2, 9)

Eis a solução:

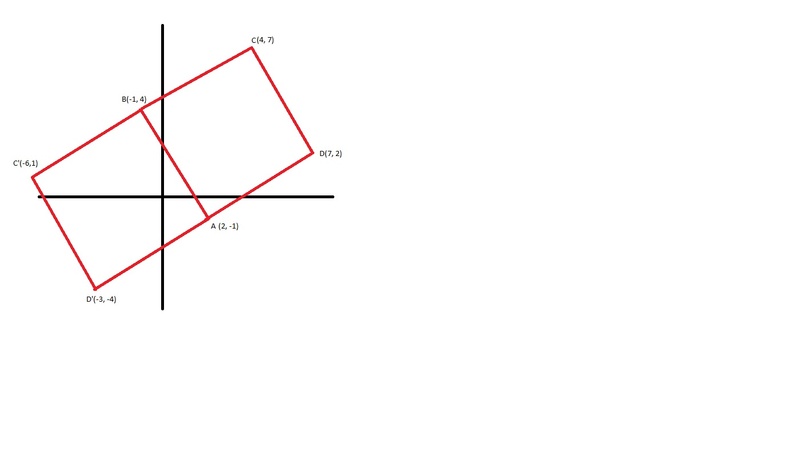
Primeiro irei transladar os pontos de tal forma que o A coincida com a origem, dessa forma iremos obter os pontos A'(0,0) e B'(-3,5), para obter o primeiro quadrado (no caso eu estou indo achar os pontos (-6,1) e (-3,-4) que estão na figura do Grande Mestre Elcioschin) lembrando que a matriz de rotação é dada por:

\begin{bmatrix}
cos(\theta) & -sen(\theta)\\
sen(\theta) & cos(\theta)
\end{bmatrix}

O ponto D' da figura do Elcioschin é bem simples de encontrar, basta fazer uma rotação de 90º no sentido anti-horário do vetor B', portanto:

\begin{bmatrix}
cos(90^{\circ}) & -sen(90^{\circ})\\
sen(90^{\circ}) & cos(90^{\circ})
\end{bmatrix}\begin{bmatrix}
-3\\
5
\end{bmatrix}=\begin{bmatrix}
-5\\
-3
\end{bmatrix}

Lembrando que havíamos transladados os pontos, então devemos somar com A para encontrarmos o vetor D', portanto D'(-5+2,-3-1) → D'(-3,-4).


Agora para o ponto C' da figura do Elcioschin, devemos fazer uma rotação de 45° no sentido anti-horário do vetor B' e depois multiplicar o vetor que encontrarmos por raiz de 2, dessa forma:


\begin{bmatrix}
cos(45^{\circ}) & -sen(45^{\circ})\\
sen(45^{\circ}) & cos(45^{\circ})
\end{bmatrix}\begin{bmatrix}
-3\\
5
\end{bmatrix}=\begin{bmatrix}
-4\sqrt{2}\\
\sqrt{2}
\end{bmatrix}

Multiplicando por raiz de 2, iremos encontrar (-8,-2), agora devemos somar com A para encontrar C', portanto C'(-8+2,2-1) → C'(-6,1).

Para encontrar os pontos C e D restantes basta rotacionar por 90º no sentido horário, ou seja, fazer θ igual a -90º na matriz de rotação e depois fazer θ = -45º e multiplicar por √2, lembrando de somar A aos vetores resultantes.