Você provavelmente já viveu a experiência de se encontrar em um veículo (trem ou automóvel) em movimento num momento em que outro veículo se emparelha com o que você está. Você olha para o lado e vê o outro imóvel, lado a lado.

Da mesma maneira, um veículo que vem em sentido oposto ao seu passa por você muito mais rapidamente que outro que o ultrapassa vindo por trás, no mesmo sentido.

Quando uma ambulância com a sirene ligada, em velocidade, passa, você tem a sensação que o som emitido pela sirene aumenta de frequência à medida em que se aproxima e reduz a frequência enquanto se afasta.

Tudo isso envolve a questão do referencial e do movimento relativo. Toda a cinemática e os movimentos relativos foram estudados pelo físico, astrônomo e matemático florentino Galileu Galilei (1546 - 1642).


 Pré-Requisitos para a relatividade de Galileu


para o estudo dos movimentos e, consequentemente da relatividade dos movimentos, é necessário apoiar-se solidamente nos conceitos de referencial, vetores e adição de vetores.

Um referencial é um sistema de coordenadas no qual está localizada a posição a partir da qual se realizam observações e medidas. Podemos considerar referenciais unidimensionais (como uma reta), bidimensionais (como um plano) ou tridimensionais (como um espaço em R3), conforme a situação exija.

Vetores são entidades matemáticas que expressam grandezas que, além de serem caracterizadas por uma medida de intensidade (comprimento, temperatura, massa, etc), requerem, para seu total entendimento, uma referência de direção e sentido em que se manifestam, como são velocidade, força, quantidade de movimento, etc.


A adição de vetores


As grandezas escalares (não vetoriais) operam matematicamente com as regras aritméticas da adição, subtração, multiplicação e divisão. Para as operações com vetores isso não será suficiente.

Uma grandeza vetorial possui uma intensidade que identifica o seu tamanho por um número que é acompanhado por uma unidade de medida, por exemplo 30 km/h. O valor absoluto desse número é chamado de módulo do vetor.

Além disso uma grandeza vetorial, velocidade, por exemplo, quando observada a partir de um referencial precisa ter sua direção e sentido também descritos. Um automóvel viajando a 80km/h numa estrada tem dois destinos possíveis a depender de para que lado viaja.

A direção e o sentido do vetor podem ser dadas por notação em escrita verbal ou matemática ou graficamente.

Quando dizemos:

"um avião voa de leste para oeste..."
"um trem vai de São Paulo ao Rio de Janeiro..."
" um ciclista se desloca do km 8 ao km 10..."

estamos fornecendo direção e sentido.

A notação matemática envolve o sistema de coordenadas considerado. Os sistemas mais usados são o cartesiano e o polar.


Notação no sistema cartesiano


os sistemas cartesianos adotam um, dois ou tres eixos, usualmente denominados x, y e z. O que faremos é associar a cada eixo um vetor unitário, isto é, um vetor que tenha a direção do eixo, seja orientado no sentido positivo do eixo e tenha módulo igual à unidade. Para evitar confusão com os nomes dos eixos esses vetores unitários, chamados versores, são representados pelas letras i, j e k, respectivamente.

Representamos os vetores por uma letra minúscula sobrecimada por uma pequena seta: 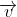. Vejamos como representar vetores num sistema cartesiano:


o módulo (ou intensidade, tamanho) do vetor 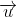da figura acima é dado pela aplicação do teorema de Pitágoras: .

Sua direção e sentido são dadas pelo coeficiente angular da reta que o suporta, ou seja, pelo ângulo que forma com o eixo horizontal no sentido anti-horário:


dessa forma ou, 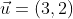 é um vetor perfeitamente caracterizado.


A notação Polar


além do cartesiano, o sistema polar é comumente utilizado. Neste sistema o vetor é caracterizado por seu tamanho (módulo) e pelo ângulo que faz, no sentido anti-horário com o eixo horizontal: