A relatividade de Galileu:
Mudanças de referencial - o movimento
relativo
pag 2
O
movimento relativo
Retornamos agora aos fenômenos descritos no
preâmbulo deste artigo. Quando um movimento é
observado, inevitavelmente essa constatação
é feita de um ponto de vista, ou referencial, onde
está localizado o observador. Podemos, na verdade,
considerar quantos e quais referenciais desejarmos.
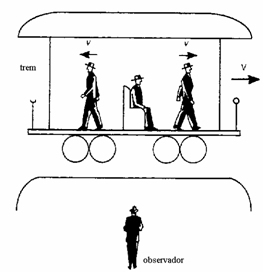
Um homem que caminha dentro de um trem em movimento pode, por exemplo,
ter seu movimento observado por uma pessoa que se encontra sentada no
mesmo trem, ou por uma pessoa em pé na plataforma, fora do
trem.
(imagem infoescola)
com
certeza cada observador o perceberá se deslocando com uma
velocidade diferente. Para a pessoa sentada no trem o homem caminha com
uma velocidade própria do caminhar, enquanto o observador na
plataforma o verá passando mais rapidamente, junto com o
trem.
Devemos a Galileu Galilei a percepção e os
estudos dessa relatividade do movimento.
Vamos esquematizar a situação descrita acima:

O homem (H) se move dentro do trem vom uma veloicidade 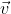 medida pelo observador sentado no trem. Esta é a sua
velocidade relativa ao referencial do trem (S'). O trem, por sua vez
tem sua velocidade medida pelo observador (O) na plataforma (S) com um
valor
medida pelo observador sentado no trem. Esta é a sua
velocidade relativa ao referencial do trem (S'). O trem, por sua vez
tem sua velocidade medida pelo observador (O) na plataforma (S) com um
valor 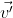 .
.
A velocidade do homem dentro do trem em relação
à plataforma é dada por:  e podemos calcular o seu módulo somando os
módulos dos vetores:
e podemos calcular o seu módulo somando os
módulos dos vetores:  .Note que se o homem dentro do trem estivesse se deslocando no sentido
oposto ao deslocamento do trem a soma vetorial ainda seria a velocidade
relativa, porém seu módulo seria expresso
por
.Note que se o homem dentro do trem estivesse se deslocando no sentido
oposto ao deslocamento do trem a soma vetorial ainda seria a velocidade
relativa, porém seu módulo seria expresso
por  .
.
Poderíamos ter grafado:
no primeiro caso: 
no segundo caso: 
no primeiro caso temos uma soma de vetores que formam entre si um
ângulo igual a zero e no segundo caso a soma de dois vetores
que formam entre si um ângulo de 180°.
Exemplo:
Um
barco desce 60 km de um rio em 1 hora e sobe o mesmo trecho em 2 horas.
Sabe-se que a potência do barco é constante, tanto
ao subir quando ao descer ao rio. Determine:
A)
A velocidade do Barco em relação ao rio
B)
A velocidade do rio em relação ás
margens
Solução:
O observador
está localizado na margem.
Quando um barco desce um rio, sua velocidade em
relação à margem é uma soma
(vetorial) das velocidades:
1)
das águas em relação à
margem
2)
do barco em relação às
águas.
60
km em 1 hora: 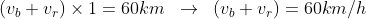
Quando
um barco sobe um rio, sua velocidade em relação
à margem é uma soma (vetorial) das velocidades:
1)
das águas em relação à
margem
2)
do barco em relação às
águas.
60
km 2m 2h: 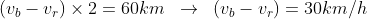

Velocidade
de aproximação e velocidade de afastamento
quando dois móveis estão dotados de velocidades
diferentes estão afastando-se ou aproximando-se.

Em todos os casos a velocidade relativa entre os móveis,
medida a partir do referencial (1) é dada por:
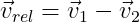
e calculamos o módulo da velocidade relativa considerando
algebricamente os módulos das velocidades.

Exemplo:
Um
avião cuja velocidade em relação ao ar
é de 400 km/h se desloca de uma cidade A para uma cidade B,
situada ao norte de A, enquanto recebe um vento de leste para oeste com
velocidade de 100 km/h em relação ao
chão. Qual a correção de rumo que o
piloto deve fazer para continuar voando em linha reta de A para B? Qual
será a sua velocidade resultante?

O
avião deve tomar um rumo nordeste fazendo um
ângulo com o norte cuja tangente é 0,25
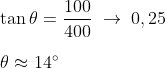
a
velocidade resultante será