ITA - círculo inscrito

Considere um triângulo isósceles ABC, retângulo em A. Seja D a intersecção da bissetriz do ângulo  com o lado BC e E um ponto da reta suporte do cateto AC de tal modo que os segmentos de reta BE e AD sejam paralelos. Sabendo que AD mede √2 cm, então a área do círculo inscrito no triângulo EBC é:

R: 4π(3 − 2√2) cm².

Abaixo está o desenho que eu fiz, com algumas anotações. Gostaria que me dissessem se até aí está correto... travei aí. :l

∠ABE e ∠DAB são alternos internos.
AB é bissetriz, mediana e altura do ∆BCE.
AB não é diâmetro, apenas contém o diâmetro.
É lógico que o ponto A é ponto de tangência da circunferência com a hipotenusa CE; você próprio anotou como "2" o valor de cada metade!

∆BCE é retângulo. Para triângulo retângulos, o raio da circunferência inscrita pode ser dado por:
r = p-a
onde a é a hipotenusa.

Aplicando a este caso,
r = 2√2 + 2 - 4 -----> r = 2(√2-1)

S = pi.r² -----> S = pi*4(2 + 1 - 2√2) -----> S = 4pi(3 - 2√2) cm²

Sim, alternos internos e AB contém o diâmetro*. Era isso que eu tinha mente, mas escrevi outra coisa, perdão.
Medeiros, ainda não consegui visualizar o que me garante que A é o ponto de tangência ia. "Instintivamente", eu consigo perceber. Mas não tô enxergando o que realmente me garante isso, desculpe. Os segmentos serem iguais me garante que é mediana... mas não tô vendo a relação com tangência. Deve ser algo bem óbvio, desculpe

Hgp2102

Em qualquer triângulo retângulo de hipotenusa a , catetos b , c e raio r do círculo inscrito, vale a relação:

2.r = b + c - a

Isto pode ser facilmente provado a partir do conhecimento de que duas tangentes a um círculo, tiradas de um ponto externo são iguais.

Na tua questão foi mostrado que b = c = 2.√2 e a = 4

2.r = 2. √2 + 2. √2 - 4 ----> 2.r = 4.√2 - 4 ----> r = 2. √2 - 2

S = pi.r² ---> S = pi.(2.V2 - 2)² ---> S = pi.(8 - 8. √2 + 4) ---> S = 4.(3 - 2. √2)

Elcio, embora pra resolver o problema não seja necessário saber que A que é o ponto de tangência, o amigo Medeiros disse que é e eu não consigo visualizar isso. O problema em si eu já entendi, o que gostaria mesmo é que me mostrassem que A é ponto de tangência.
À propósito, Elcio, se puder ver um tópico que postei na parte de eletrodinâmica do fórum sobre o método da oposição, eu agradeço  

... que A que é o ponto de tangência, o amigo Medeiros disse que é e eu não consigo visualizar isso.

Hgp, para quem se dedica à geometria, essa visualização é imediata e expontânea, decorre da própria simetria da figura. Em todo o caso, vou tentar descrever isso pormenorizadamente.

1)
∆ABC é isósceles de base BC e AD é bissetriz do âng. A:
⇒ AD também é altura e mediana referente a esse mesmo vértice.
⇒ D é ponto médio de BC.

2)
∆BCE é retângulo em B:
⇒ ∆BCE ~ ∆ABC.
⇒ ∆BCE é isósceles de base CE.

BE // AD ⇒ BE = 2.AD
⇒ A é ponto médio de CE

Ora, um círculo inscrito num triângulo isósceles, obrigatoriamente será tangente ao ponto médio da base. [se o triângulo fosse equilátero, o círculo seria tangente ao ponto médio dos três lados]

Hgp2102

O círculo é inscrito no triângulo CBE, logo tangencia os catetos e a hipotenusa

O triângulo BCE é isósceles ----> BC = BE. Além disso AB temo mesmo valor dos catetos 

Logo, o ponto A é o ponto médio de CE e é o ponto de tangência

Obrigado, senhores. Agora consegui visualizar perfeitamente. Embora seja aquilo mesmo que o Medeiros disso, que é algo óbvio para quem estuda geometria. O problema é que eu fico, às vezes, em dúvida do que eu posso ou não afirmar em geometria porque tem coisas que parecem e não são e, mesmo quando são, não me sinto bem as fazendo sem saber justificar porque são. Mais uma vez, obrigado

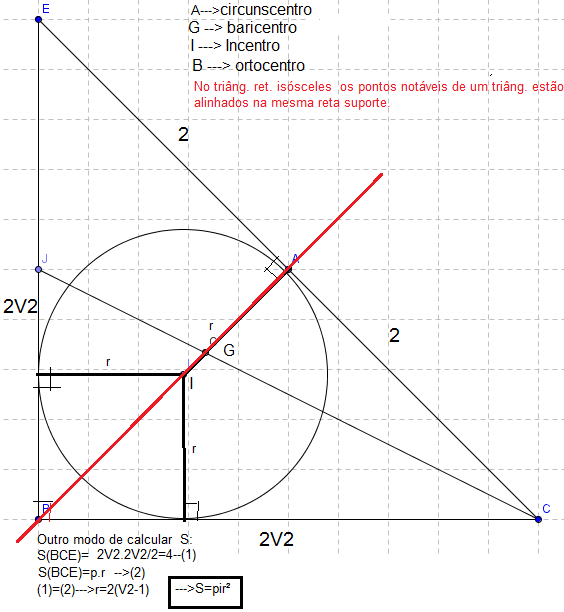
Postando a figura paras melhor visualização das explicações do mestre e do Medeiros.