Soma da Série Geométrica

por marcoscastro87 Qui 03 Jun 2010, 00:02

Olá, gostaria de saber se alguém consegue fazer essa questão de cálculo de soma da série geométrica:

Soma da Série Geométrica Serier

Eu sei que para calcular a soma da série geométrica é que nem a soma dos termos de uma PG infinita que é S=a1/(1-q), onde a1 é o primeiro termo da sequência e "q" é a razão, no caso dessa série ela está alternada, mas não consigo ver uma PG aí, ficaria muito grato caso me dessem alguma dica, valeu!

por **Euclides** Qui 03 Jun 2010, 00:09

Péra aí marcos: só com dois têrmos não dá prá saber nada!!

Prá ter uma PG os sinais têm de se alternar e aí há um têrmo negativo, um positivo e a sugestão de outro positivo.

Veja lá se é isso:

$\\-\frac{3}{4}+\frac{5}{4}-\frac{7}{4}...=\frac{1}{4}\left ( -3+5-7... \right )=\frac{1}{4}\left (-3-7-11...+5+9+13... \right )\\\\\frac{1}{4}\left ((-4n+1)+(4n+1) \right )=\frac{1}{2}$

por marcoscastro87 Qui 03 Jun 2010, 01:08

E aí cara, pois é, a questão só veio com 2 termos, ae pela lógica informal eu presumi do jeito que vc imaginou aí tb. Eu não consegui entender o seu jeito de fazer, porque, por exemplo, eu fiz uma questão que era: -2/3 + 2/9 -2/27 +.... , eu separei ela em 2 PG, fiz a soma de cada uma e depois fiz a soma final somando as duas. No caso dessa questão não daria para sair fazendo pela fórmula lá da PG infinita? Tem alguma forma geral para fazer por esse seu método ou é mesmo "arrumando" os termos de acordo com cada questão? Valeu

por **Euclides** Qui 03 Jun 2010, 01:11

Da maneira como eu escrevi são Duas PA's e não PG's. Com dois termos pode ser qualquer coisa, inclusive pode nem ser uma série

3, 1873 é serie? é PG? é PA?

por marcoscastro87 Qui 03 Jun 2010, 01:18

pois é, tou viajando na maionese, mas quando fala de soma de série geométrica ele sempre tá falando de uma PG né

por **Euclides** Qui 03 Jun 2010, 01:24

Olha, se aquilo é uma PG:

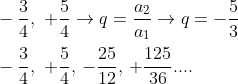
$\\-\frac{3}{4},\,\,+\frac{5}{4}\to q=\frac{a_2}{a_1}\to q=-\frac{5}{3}\\\\-\frac{3}{4},\,\,+\frac{5}{4},\,-\frac{25}{12},\,+\frac{125}{36}....$

por **Euclides** Qui 03 Jun 2010, 01:36

continuando:

$\\-\frac{3}{4},\,\,+\frac{5}{4}\to q=\frac{a_2}{a_1}\to q=-\frac{5}{3}\\\\-\frac{3}{4},\,\,+\frac{5}{4},\,-\frac{25}{12},\,+\frac{125}{36}....\\\\ -\frac{3}{4}+\sum_{1}^{\infty}\frac{(-5)^n}{4.3^{(n-1)}}$