Geometria do espaço-tempo

Tenho uma duvida com relação a geometria do espaço-tempo: de acordo com a relatividade a gravidade é resultado das distorções que altas concentrações de matéria produzem no espaço. Sendo assim um corpo esférico, como o sol por exemplo, deveria gerar em torno de si uma dobra também esférica e os demais corpos "menores" movimentam-se através desta dobra no espaço. Sendo assim a orbita da terra não deveria ser circular ou invés de elíptica ?

Em primeiro lugar, se as órbitas são elípticas é porque não deveriam ser círculos perfeitos.

Note que:

- o espaço-tempo é uma circunstância quadri-dimensional e uma esfera é uma inferência tridimensional.

- o Sol, a Terra, todos os planetas e estrelas estão em constante movimento e suas posições relativas mudam constantemente

- todas essas massas têm sua contribuição na geometria do espaço-tempo.

Excelente pergunta Marcelo. Tudo que o Euclides escreveu está certo mas espero que isso também te ajude. 
 
  A verdade é que de acordo com a relatividade geral o que se tem não é exatamente uma elipse. A elipse não se fecha perfeitamente. Vinte anos de observação a mercúrio, onde o efeito é mais óbvio no sistema solar, já provaram essa tese: http://www.e-escola.pt/topico.asp?id=588&ordem=3
Órbitas não circulares, como do planeta Mercúrio, seguem caminhos que não seriam os esperados pela mecânica clássica. Seria como o caso das partículas que ultrapassam o horizonte de eventos e caem para sempre dentro de um buraco negro, porém o caso de Mercúrio é mais tênue, já que ele não mergulha dentro do Sol. O que é observado no caso deste planeta é que sua órbita é uma elipse bem excêntrica, sendo que o mesmo realiza um movimento de precessão em torno do Sol.
  A relatividade não é uma teria simples de interpretar sem o auxílio matemático. E esse auxílio também não é dos mais simples. Não funciona exatamente como os documentários que só mostram um plano e nem se quer mostram a interferência da distorção temporal. Você deve imaginar que o espaço sofrendo curvatura como uma bolha parada dentro da água. 

  Lembra do teorema de pitágoras? S^2=a^2+b^2, ou como preferir. Ele te da o comprimento de uma reta, com catetos a e b. O fato é que não existem retas no universos. Mas essa sempre é a referência local. Lembre-se do mapa da terra, um mapa com projeção cilíndrica. Por que os paralelos são curvos? E os meridianos retos? Distorções. Ambas as linhas se encaixam como geodésicas, linhas que representam as distâncias mínimas. Mas aqui do chão, tudo parece ser uma linha reta. Parece que a terra é realmente chata.
  Agora se estamos no espaço vemos os aviões descreverem círculos máximos, considerando que a terra é uma esfera perfeita. Esta é a posição na qual compendiários o nosso universo. Você não já se perguntou, o espaço curva-se em relação a que? Dentro de que? Por que? As duas primeiras perguntas são respondidas pelo fato Relatividade.
   Não é exatamente uma curvatura, é uma mudança de escala que varia continuamente. Voltemos ao exemplo da terra. Imagine que exista um morro imenso na frente da sua casa e que você tenha que subir e descer para chegar no trabalho indo em linha reta, euclidianamente, ou pode dar a volta o que seria até um caminho mais curto. A segunda opção exemplifica uma linha geodésica. 
  Mas então, porque órbita elípticas e não circulares? Interessante, no modelo Newtoniano são possíveis orbitas circulares. A justificativa que ele deu a sua não existência é a improbabilidade. É necessária uma condição específica de posicionamentos e massas para que se tenha o efeito. Em um universo com tantas possibilidades temos a chance de 1 para infinito, ou seja, nulo. Mas essa seria a chance para qualquer configuração, que seria impossível? Por isso talvez exista uma partícula indivisível, ou seja, não existem infinitas configurações, mas continua improvável.

  O mesmo é valido para a relatividade. É possível mais improvável a ocorrência de uma órbita perfeitamente circular. Um centro massivo esfericamente distribuído é descrito pela métrica de  Swarzstchild:



Onde estamos basicamente escrevendo um teorema de Pitágoras em coordenadas esféricas. Mas existe um fator diferencial: O tempo!   

 Voltemos ao nosso exemplo em que observamos do espaço nossos ciadões andando em círculos. A terra não gira? Exatamente isso. Imagine a imagem do globo terrestre com todos seus paralelos e meridianos girando em torno de si mesmo. Imagine que observamos homens primitivos tentando viajar lentamente. Eles querem chagar exatamente no "outro lado do mundo". digamos no ponto simétrico exato em relação à eles em seu ponto atual. Se a terra estivesse parada tanto faz andar para um lado ou para o outro. Mas se ela gira compensa mais andar contra a sua rotação que a favor. Não gastaria menos tempo? Vamos supor que eles tenham um conceito do que é reta e que façam um mapa da terra considerando que reta é o seguimento em que se leva menos tempo para andar. 

  Pense no mapa distorcido que eles fariam. As curvas representadas seriam as linhas geodésicas, ou seja, as órbitas. Elas se parecem com os paralelos convencionais? Essa é a diferença entre uma órbita circular e elíptica, mas não existe um ponto de onde observamos todo o universo. Se estamos em 3d+ tempo, considerando a relatividade geral, a "distância" que deve ser minimizada para que tenhamos uma geodésica é:

S^2=c^2 t^2+x^2+y^2+z^2

Onde c é a velocidade da luz é t o tempo (x,y,z) as coordenadas. A equação da órbita seria:


E tudo isso é pura geometria, onde a matéria diz se você está em cima de um plano, cilindro, esfera, ou seja o que for. Tudo isso é mudado pelo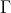 (gama) chamado simbolo de Cristofel.


  Imagine no exemplo da terra denovo. Não com a terra esférica mais com um cilindro regular. Se ele
gira na velocidade da luz, usando a relatividade restrita, você não pode seguir em uma das direções(qual?). É o que ocorre com um buraco negro a partir do horizonte  de eventos.

  A título de curiosidade:
Uma partícula em órbita sob a métrica de Schwarzschild pode ter uma órbita circular estável caso:

R>2GM/c^2

onde R é o raio do "sol" no nosso caso.


O problema é que para tal R, a estrela é super densa. É um buraco negro pra ser exato uma distorção máxima do espaço. Imagine no caso do cilindro. Se fizéssemos um mapa, como representaríamos ser impossível seguir uma direção? O mapa com certeza seria partido naquele ponto. Mas porque então as coisas não ficam orbitando um buraco negro sem nunca "cair"?

O problema é que não se trata de um ponto. Essa distorção também varia com o espaço, e os objetos passam a ter velocidades e afetar nessa distorção. O universo é um sistema caótico, e tudo vai para dentro de um buraco negro.