Máximo e Mínimo
3 participantes
Página 1 de 1
Máximo e Mínimo
por Kassia da Silva Qua 16 Abr 2014, 15:23
Por favor estou em dificuldade nesta questão:
Suponha que a função f seja derivável até a segunda ordem em R e tal que para todo x que pertence a R
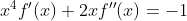
a)Se f possui um máximo relativo em a, prove que
b)Se f possui um mínimo relativo em b, prove que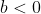
Desde já muito obrigada.
Suponha que a função f seja derivável até a segunda ordem em R e tal que para todo x que pertence a R
a)Se f possui um máximo relativo em a, prove que
b)Se f possui um mínimo relativo em b, prove que
Desde já muito obrigada.
Kassia da Silva- Iniciante
- Mensagens : 28
Data de inscrição : 26/04/2013
Idade : 36
Localização : Petrópolis ,RJ<Brasil
Re: Máximo e Mínimo
por Man Utd Qua 16 Abr 2014, 16:27
Olá 
Primeiro perceba que :
+2xf^{\prime&space;\prime&space;}(x)=-1&space;\\\\\\&space;\left(&space;x^4*f^{\prime}(x)\right)^{\prime}=-1&space;\\\\\\&space;x^4*f^{\prime}(x)=-x+C&space;\\\\\\&space;f^{\prime}(x)=-\frac{1}{x^3}+\frac{C}{x^4})
os pontos críticos "a" e "b" saem do zero da primeira derivada, isto é :
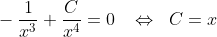, obs: o valor de "x" representa o valor de "a" e "b" dependendo do sinal de "C" .
Agora a segunda derivada da função fica :
=-1&space;\;\;\;&space;\Rightarrow&space;\;\;&space;f^{\prime&space;\prime}(x)=-\frac{1}{2C})
lembrando que f'(x)=0, pois estamos supondo que x é um ponto crítico.Então se C>0 , teremos f''(x)<0 então pelo teste da segunda derivada é um ponto de máximo,como C=x=a, então "a" é maior que zero.Agora para c<0 temos que f''(x)>0, então pelo teste da segunda derivada obtemos que é um ponto de mínimo e isto implica que C=x=b, então "b" é menor que zero.
Primeiro perceba que :
os pontos críticos "a" e "b" saem do zero da primeira derivada, isto é :
Agora a segunda derivada da função fica :
lembrando que f'(x)=0, pois estamos supondo que x é um ponto crítico.Então se C>0 , teremos f''(x)<0 então pelo teste da segunda derivada é um ponto de máximo,como C=x=a, então "a" é maior que zero.Agora para c<0 temos que f''(x)>0, então pelo teste da segunda derivada obtemos que é um ponto de mínimo e isto implica que C=x=b, então "b" é menor que zero.
Man Utd- Grupo
Velhos amigos do Fórum
- Mensagens : 1119
Data de inscrição : 18/08/2012
Idade : 30
Localização : Manchester
Re: Máximo e Mínimo
por BETA ALFA Ter 22 Abr 2014, 17:58
olá, estou com muita dificuldade de entender este exercício,se puder me ajudar agradeço muito. 1ºcomo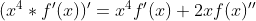 
,tentei derivar 
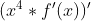e deu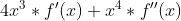 
. 
BETA ALFA- Padawan
- Mensagens : 70
Data de inscrição : 15/08/2013
Idade : 40
Localização : TERESOPOLIS-RJ-BRASIL
Re: Máximo e Mínimo
por Man Utd Ter 22 Abr 2014, 21:37
BETA ALFA escreveu:olá, estou com muita dificuldade de entender este exercício,se puder me ajudar agradeço muito. 1ºcomo
Vc está certo, fui eu que errei.foi mal.
Vamos tentar de outro jeito :
Vamos aplicar o ponto "a" na função :
Sabemos que se "a" for um ponto de min ou máx, teremos obrigatoriamente f'(a)=0, então :
Se a>0 , temos que f''(a)<0 logo pelo teste da segunda derivada este é um ponto de máximo.
analogamente para "b" :
se b<0 temos que f''(b)>0, logo pelo teste da segunda derivada este é um ponto de mínimo.
Man Utd- Grupo
Velhos amigos do Fórum - Mensagens : 1119
Data de inscrição : 18/08/2012
Idade : 30
Localização : Manchester
Tópicos semelhantesPágina 1 de 1
Permissões neste sub-fórum
Não podes responder a tópicos
