(Unesp) Cone
2 participantes
Página 1 de 1
(Unesp) Cone
por perlingra Sáb 08 Mar 2014, 12:29
:No trapézio ABCD da figura a seguir, os ângulos internos em A e B são retos, e o ângulo interno em D é tal que sua tangente vale 5/6. Se AD = 2 . AB, o volume do sólido obtido ao se girar o trapézio em torno da reta por B e C é dado por:
a) (3/4) (Pi)a³
b) (5/ 8 ) (Pi)a³
c) (6/5) (Pi)a³
d) (20/13) (Pi)a³
e) (8/5) (Pi)a³
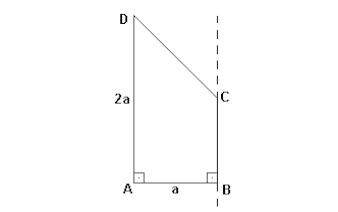
Eu dividi o trapézio em duas partes, o triângulo com hipotenusa DC e o quadrilátero ... Só que to com com muita dificuldade para entender qual ser o sólido formado pela rotação desse triângulo
a) (3/4) (Pi)a³
b) (5/ 8 ) (Pi)a³
c) (6/5) (Pi)a³
d) (20/13) (Pi)a³
e) (8/5) (Pi)a³
Eu dividi o trapézio em duas partes, o triângulo com hipotenusa DC e o quadrilátero ... Só que to com com muita dificuldade para entender qual ser o sólido formado pela rotação desse triângulo
Última edição por perlingra em Sáb 08 Mar 2014, 12:32, editado 1 vez(es)
perlingra- Recebeu o sabre de luz
- Mensagens : 154
Data de inscrição : 16/08/2012
Idade : 28
Localização : São Luís, MA, Brasil
Re: (Unesp) Cone
por Elcioschin Sáb 08 Mar 2014, 13:02
Você não está seguindo o que eu te ensinei VÁRIAS vezes
Considere a reta que contém BC como um espelho
Desenhe a imagem A'BCD' do trapézio
O volume do sólido é a diferença entre o volume do cilindro de raio AB = A'B = a e altura AD = 2a e o volume do cone de mesmo raio e altura h = AD - BC = a - BC
Para calcular BC:
tgD = AB/(AD - BC) ----> 5/6 = a/(2a - BC) ----> Calcule BC em função de a
Considere a reta que contém BC como um espelho
Desenhe a imagem A'BCD' do trapézio
O volume do sólido é a diferença entre o volume do cilindro de raio AB = A'B = a e altura AD = 2a e o volume do cone de mesmo raio e altura h = AD - BC = a - BC
Para calcular BC:
tgD = AB/(AD - BC) ----> 5/6 = a/(2a - BC) ----> Calcule BC em função de a
Elcioschin- Grande Mestre
- Mensagens : 73164
Data de inscrição : 15/09/2009
Idade : 78
Localização : Santos/SP
Re: (Unesp) Cone
por perlingra Sáb 08 Mar 2014, 13:08
Eu sei que você me ensinou várias vezes, só demorei para entender ... Obrigada!Elcioschin escreveu:Você não está seguindo o que eu te ensinei VÁRIAS vezes
Considere a reta que contém BC como um espelho
Desenhe a imagem A'BCD' do trapézio
O volume do sólido é a diferença entre o volume do cilindro de raio AB = A'B = a e altura AD = 2a e o volume do cone de mesmo raio e altura h = AD - BC = a - BC
Para calcular BC:
tgD = AB/(AD - BC) ----> 5/6 = a/(2a - BC) ----> Calcule BC em função de a
perlingra- Recebeu o sabre de luz
- Mensagens : 154
Data de inscrição : 16/08/2012
Idade : 28
Localização : São Luís, MA, Brasil
Tópicos semelhantes» Cone - UNESP 2014
» (Unesp) cilindro e cone
» Volume tronco de cone e cone de mesma altura
» Cone e Tronco de Cone
» Cone em um tronco de cone
» (Unesp) cilindro e cone
» Volume tronco de cone e cone de mesma altura
» Cone e Tronco de Cone
» Cone em um tronco de cone
Página 1 de 1
Permissões neste sub-fórum
Não podes responder a tópicos
