Problema do ITA sobre funções?

por julia.rezende Dom 23 Jun 2013, 18:29

No sistema de coordenadas cartesianas ortogonais, a curva y= ax^2 + bx + c passa pelos pontos (1;1), (2;m), (m;2), onde m é um número real diferente de 2. Sobre esta curva, podemos afirmar que:
a) Ela admite um mínimo para todo m tal que 1/2 < m < 3/2
b) Ela admite um mínimo para todo m tal que 0 < m < 1
c) Ela admite um máximo para todo m tal que -1/2 < m < 1/2

Gabarito letra B. Obrigada desde já.

por Rock6446 Seg 24 Jun 2013, 23:03

Como a questão envolve máximo e mínimo, temos que analisar "a" e "m", de forma que restem apenas os dois números numa mesma equação. Assim, montando um sistema com os pontos dados:
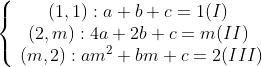
$Problema do ITA sobre funções? Gif.latex?%5Cleft%5C%7B%5Cbegin%7Bmatrix%7D%20%281%2C1%29%3Aa+b+c%3D1%28I%29%5C%5C%20%282%2Cm%29%3A4a+2b+c%3Dm%28II%29%5C%5C%20%5C%2C%5C%2C%28m%2C2%29%3Aam%5E2+bm+c%3D2%28III%29%20%5Cend%7Bmatrix%7D%5Cright$

Subtraindo II de I, temos:

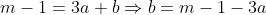
$Problema do ITA sobre funções? Gif$

Subtraindo III de I, temos:

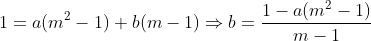
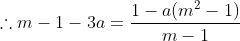
$Problema do ITA sobre funções? Gif$

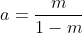
$Problema do ITA sobre funções? Gif$

Manipulando algebricamente, você encontrará

$Problema do ITA sobre funções? Gif$

Agora basta analisar as alternativas dadas. Lembrando que:

a > 0: existe um mínimo; a < 0: existe um máximo.

Se 0 < m < 1, ela vai admitir um mínimo, pois "a" fica positivo. Bate exatamente com a letra b)

Qualquer dúvida, por favor diga.

Problema do ITA sobre funções?

Problema do ITA sobre funções?

Re: Problema do ITA sobre funções?

Um fórum livre e democrático.