ABCD é um quadrado e o ∆CEF é equilátero

por Nat' Sex 14 Set 2012, 16:59

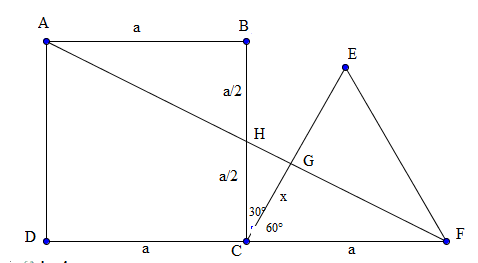
ABCD é um quadrado e o ∆CEF é equilátero, ambos de lado a. Unindo A e F obtemos um segmento CG no lado CE. Calcule a medida do segmento CG em função de a.

Figura:
[url=https://i.imgur.com/oU6QX.jpg ]https://i.imgur.com/oU6QX.jpg [/url]

Resp. CG = 2a(2√3 - 1)/11

por **Elcioschin** Sex 14 Set 2012, 17:56

Fazendo por GA

Seja um sistema xOy com origem em D(0, 0). Temos os seguintes pontos:

A(0, a) ----> F(2a, 0) ----> C(a, 0) -----> E(3a/2, a*\/3/2)

a) Determine a equação da reta AF ----> y = mx + n
b) Idem da reta CE ----> y = x + q
c) Iguale ambas e calcule xG e depois calcule yG -----> G(xG, yG)
d) Cacule CG ----> CG² = (xG - xC)² + (yG - yC)²

por Nat' Sex 14 Set 2012, 21:20

Obrigada!

por **raimundo pereira** Qui 01 Nov 2012, 20:47

por **raimundo pereira** Qui 01 Nov 2012, 21:52

abcd e um quadrado - ABCD é um quadrado e o ∆CEF é equilátero Abj9f7

Outro modo???
da semelhança dos triângulos FHC e AFD temos BH=HC=a/2
S∆ GFC + S∆GHC = S∆HFC

(a*x*sen60°)/2 + (a/2*x*sen30°)/2= (a/2 * a)/2

(a*x*V3/2)/2 + (a/2*x *1/2)/2= a²/4

a*xV3/4 + a*x/4=a²/4

a*xV3 +a*x=a²
a*x(V3+1)=a²
x=a/V3+1
x=a(V3-1)/2

O que não bate com o gab. Onde errei ?

por **Elcioschin** Sex 02 Nov 2012, 11:51

Raimundo

O erro foi na passagem da 2ª para a 3ª linha. A 3ª linha correta é:

a*x*\/3/4 + ax/8 = a²/4

2ax*\/3 + ax = 2a² ----> x*(2*\/3) + x = 2a ----> x*(2*\/3 + 1) = 2a ----> x = 2a/(2*\/3 + 1) ---->

x = 2a*(2*\/3 - 1)/11 ----> Confere com o gabarito