Sistema de Equações
3 participantes
PiR2 :: Matemática :: Álgebra
Página 1 de 1
 Sistema de Equações
Sistema de Equações
Quem saberia resolver este sistema:
x - y)(x² - y²) = xy - 729
(x + y)(x² + y²) = xy + 209871
Desde já, muito obrigado.
Um abraço!
x - y)(x² - y²) = xy - 729
(x + y)(x² + y²) = xy + 209871
Desde já, muito obrigado.
Um abraço!

ivomilton- Membro de Honra

- Mensagens : 4994
Data de inscrição : 08/07/2009
Idade : 92
Localização : São Paulo - Capital
 SISTEMA DE EQUAÇÕES
SISTEMA DE EQUAÇÕES
Olá,senhor ivomilton.
![(x-y)(x^2-y^2)=xy-729\\\\ (x+y)(x^2+y^2)=xy+209871\\\\(x-y)(x+y)(x-y)=xy-729\\\\(x+y)[(x+y)^2-2xy)]=xy+209871\\\\(x-y)^2)(x+y)=xy-729\\\\(x+y)^3-2xy(x+y)=xy+209871](http://latex.codecogs.com/gif.latex?(x-y)(x^2-y^2)=xy-729\\\\ (x+y)(x^2+y^2)=xy+209871\\\\(x-y)(x+y)(x-y)=xy-729\\\\(x+y)[(x+y)^2-2xy)]=xy+209871\\\\(x-y)^2)(x+y)=xy-729\\\\(x+y)^3-2xy(x+y)=xy+209871)
Subtraindo a 2º equação da 1ª teremos:
^3-2xy(x+y)-(x-y)^2(x+y)=210600)
Vamos colocar o fator (x+y) em evidência
![(x+y)[(x+y)^2-2xy-(x-y)^2]=210600\\\\(x+y)[x^2+2xy+y^2-2xy-(x^2-2xy+y^2)]=210600\\\\(x+y)[x^2+y^2-x^2+2xy-y^2]=210600\\\\2xy(x+y)=210600\\\](http://latex.codecogs.com/gif.latex?(x+y)[(x+y)^2-2xy-(x-y)^2]=210600\\\\(x+y)[x^2+2xy+y^2-2xy-(x^2-2xy+y^2)]=210600\\\\(x+y)[x^2+y^2-x^2+2xy-y^2]=210600\\\\2xy(x+y)=210600\\\)
Utilizando as duas incógnitas (a) e (b) teremos:
=a)
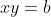

^3-2xy(x+y)=xy+209871)
=\frac{105000}{a}+209871\\\\a^3-210000=\frac{105000}{a}+209871\\\\a^4-419871a=105000\\\\a(a^3-419871)=105000)
Vou deixar o restante pra quem quiser continuar.
Subtraindo a 2º equação da 1ª teremos:
Vamos colocar o fator (x+y) em evidência
Utilizando as duas incógnitas (a) e (b) teremos:
Vou deixar o restante pra quem quiser continuar.
adriano tavares- Grande Mestre

- Mensagens : 600
Data de inscrição : 25/07/2009
Localização : São Paulo
 Re: Sistema de Equações
Re: Sistema de Equações
2xy*(x + y) = 210 600
xy(x + y) = 105 300
xy(x + y) = 2²*3²*5²*117
Pesquisa dos divisores intermediários -----> xy*(x + y) = 1404*75
x + y = 75 ----> x = 75 - y
xy = 1404 ----> x*(75 - x) = 1404 ----> x² - 75x + 1404 = 0 ----> Raízes x = 36 e x = 39
xy(x + y) = 105 300
xy(x + y) = 2²*3²*5²*117
Pesquisa dos divisores intermediários -----> xy*(x + y) = 1404*75
x + y = 75 ----> x = 75 - y
xy = 1404 ----> x*(75 - x) = 1404 ----> x² - 75x + 1404 = 0 ----> Raízes x = 36 e x = 39

Elcioschin- Grande Mestre

- Mensagens : 73164
Data de inscrição : 15/09/2009
Idade : 78
Localização : Santos/SP
 Sistema de Equações
Sistema de Equações
Aos amigos Adriano e Elcio, os meus parabéns pela resolução em conjunto de minha questão sobre sistema de equações!
Fico-lhes muito agradecido pelo excelente trabalho, pois a mesma estava completando um ano neste mês, e vocês conseguiram resolvê-la em valores inteiros de "x" e "y".
Essa questão foi-me passada por um amigo e, na ocasião, resolvi da seguinte forma:
------------------------------------------------------------------------------------
1º) Desenvolvi os primeiros membros de cada equação:
(x - y)(x² - y²) = xy - 729
(x + y)(x² + y²) = xy + 209871
x³ - x²y - xy² + y³ = xy - 729 ........... [1]
x³ + x²y + xy² + y³ = xy + 209871 ..... [2]
A seguir, multipliquei [1] por (-1) e adicionei à [2]:
(Coloquei sinal (+) mesmo onde era desnecessário, a fim de melhor posicionar os termos)
- x³ + x²y + xy² - y³ = - xy + 729
+ x³ + x²y + xy² + y³ = + xy + 209871
-------------------------------------
..... + 2x²y + 2xy² ... = .... + 210600
Simplifiquei ambos os membros por 2:
x²y + xy² = 105300
Colocando "xy" em evidência, ficou:
xy.(x+y) = 105300
Os valores de "x" e de "y" poderiam estar próximos ou distantes um do outro.
Considerei que seus valores estivessem o mais próximo possível; a princípio, considerei-os iguais:
x=y
xy = x.x = x²
x+y = x+x = 2x
Assim, transformei
xy.(x+y) = 105300
em
x².(2x) = 105300
2.x³ = 105300
x³ = 105300/2 = 52650
x = ³√52650 = 37,48
x² = (37,48)²= 1404,75
2x = 2*37,48 = 74,96
Continuando, arredondei este último para 75 e calculei quanto ficaria para o outro fator:
105300/75 = 1404
√1404 = 37,47
Como estava querendo fazer x=y, seus valores (se esta fosse a solução) iriam girar ao redor de 37,47.
De fato, 1404 = 36 x 39
E 36 + 39 = 75
Então, os valores de "x" e "y" que satisfazeram ao sistema foram:
x = 36 ; y = 39 (ou vice-versa: x = 39 ; y=36)
Foi uma coincidência tê-las obtida assim, de pronto; claro!
------------------------------------------------------------------------------------
Por ter havido, então, essa coincidência, resolvi colocar a questão no site, e aguardar que alguém tivesse uma solução mais adequada.
E foi o que vocês agora, em conjunto, conseguiram.
Mais uma vez, os meus parabéns!
O Senhor lhes dê uma abençoada semana!
Fico-lhes muito agradecido pelo excelente trabalho, pois a mesma estava completando um ano neste mês, e vocês conseguiram resolvê-la em valores inteiros de "x" e "y".
Essa questão foi-me passada por um amigo e, na ocasião, resolvi da seguinte forma:
------------------------------------------------------------------------------------
1º) Desenvolvi os primeiros membros de cada equação:
(x - y)(x² - y²) = xy - 729
(x + y)(x² + y²) = xy + 209871
x³ - x²y - xy² + y³ = xy - 729 ........... [1]
x³ + x²y + xy² + y³ = xy + 209871 ..... [2]
A seguir, multipliquei [1] por (-1) e adicionei à [2]:
(Coloquei sinal (+) mesmo onde era desnecessário, a fim de melhor posicionar os termos)
- x³ + x²y + xy² - y³ = - xy + 729
+ x³ + x²y + xy² + y³ = + xy + 209871
-------------------------------------
..... + 2x²y + 2xy² ... = .... + 210600
Simplifiquei ambos os membros por 2:
x²y + xy² = 105300
Colocando "xy" em evidência, ficou:
xy.(x+y) = 105300
Os valores de "x" e de "y" poderiam estar próximos ou distantes um do outro.
Considerei que seus valores estivessem o mais próximo possível; a princípio, considerei-os iguais:
x=y
xy = x.x = x²
x+y = x+x = 2x
Assim, transformei
xy.(x+y) = 105300
em
x².(2x) = 105300
2.x³ = 105300
x³ = 105300/2 = 52650
x = ³√52650 = 37,48
x² = (37,48)²= 1404,75
2x = 2*37,48 = 74,96
Continuando, arredondei este último para 75 e calculei quanto ficaria para o outro fator:
105300/75 = 1404
√1404 = 37,47
Como estava querendo fazer x=y, seus valores (se esta fosse a solução) iriam girar ao redor de 37,47.
De fato, 1404 = 36 x 39
E 36 + 39 = 75
Então, os valores de "x" e "y" que satisfazeram ao sistema foram:
x = 36 ; y = 39 (ou vice-versa: x = 39 ; y=36)
Foi uma coincidência tê-las obtida assim, de pronto; claro!
------------------------------------------------------------------------------------
Por ter havido, então, essa coincidência, resolvi colocar a questão no site, e aguardar que alguém tivesse uma solução mais adequada.
E foi o que vocês agora, em conjunto, conseguiram.
Mais uma vez, os meus parabéns!
O Senhor lhes dê uma abençoada semana!

ivomilton- Membro de Honra

- Mensagens : 4994
Data de inscrição : 08/07/2009
Idade : 92
Localização : São Paulo - Capital
 Tópicos semelhantes
Tópicos semelhantes» Sistema de equações
» Sistema de equacoes
» sistema de equaçoes
» Sistema de equações em Z
» Sistema de equações
» Sistema de equacoes
» sistema de equaçoes
» Sistema de equações em Z
» Sistema de equações
PiR2 :: Matemática :: Álgebra
Página 1 de 1
Permissões neste sub-fórum
Não podes responder a tópicos












