Área total de um cilindro reto

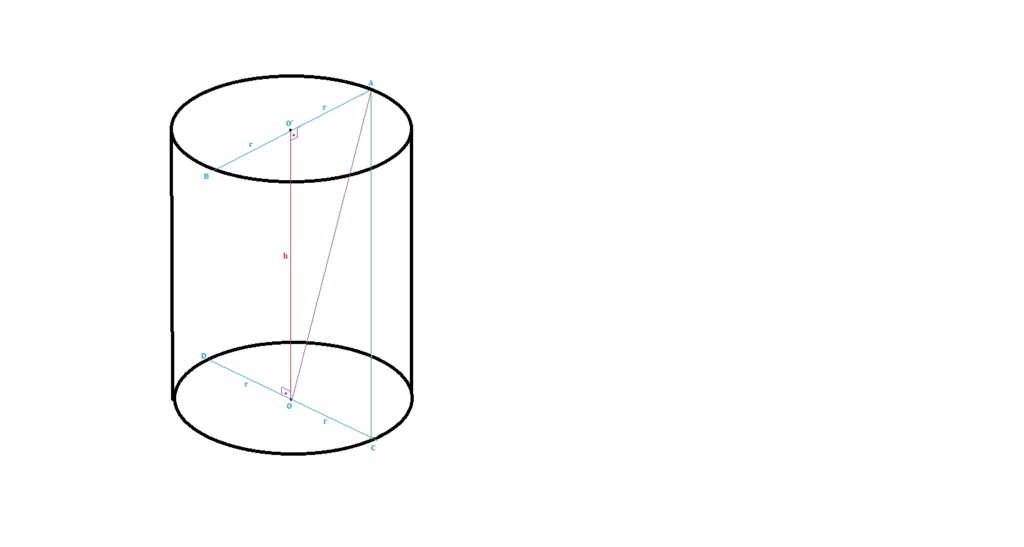
O diâmetro AB da base superior de um cilindro reto é ortogonal ao diâmetro CD da base inferior. Sendo AC = 10 cm e sabendo que a distância do segmento AC ao eixo do cilindro é 4 cm, calcule a área total do cilindro.

\(Resp.: 16 \pi (4+3\sqrt2) cm^2 \)

Se possível, poderiam fazer um desenho? Não estou conseguindo visualizar esse enunciado. Tentei fazê-lo no papel, mas não consigo enxergar muita coisa.

Acredito que a figura é esta:

Evidentemente AC corre por dentro do cilindro.
OO' = eixo do cilindro
AB e CD = ortogonais, i.e., reversas perpendiculares
AC e OO' = reversas
AC = 10 cm

A distância de AC ao eixo OO' é PQ = 4 cm. A distância entre retas reversas é medida na perpendicular comum a ambas e na menor distância entre elas. Dado que os segmentos têm extremos nas bases do cilindro, essa distância ocorrerá na metade da altura do cilindro. Indiquei o corte do plano que secciona nesta altura por λ.



Pitágoras em:
1) ∆AA'O'  --->  AO'² = AA'² + AO'²  ----->   AO'² = h² + r²  ................(I)
2) AO' está no plano axial ABB'A', logo é perpendicular a CD.
∆AO'C  --->  AO'² = AC² - CO'²  ----->  AO'² = 10² - r²  ......................(II)
(I) = (II):  100 - r² = h² + r²  ----->  h² = 100 - 2r²  .............................(III)

plano λ
por Pitágoras  ----->  r = 4√2 cm  ................................(IV)
(4) em (3):  h² = 100 - 2.(4√2)²  ----->  h² = 100 - 64  ----->  h = 6 cm

S = 2.(πr²) + 2πr.h  ----->  S = 2π(4√2)² + 2π(4√2).6  ----->  S = 64π + 48√2.π