Perímetro da figura

Relembrando a primeira mensagem :

(UESC-BA) No processo inicial de criação de um logotipo para uma empresa, um designer esboçou várias composições de formas geométricas, na tentativa de encontrar algo simples e representativo. Em uma dessas composições, um círculo de raio r = 6 cm foi sobreposto a um triângulo equilátero de lado L = 18 cm, de acordo com a figura.



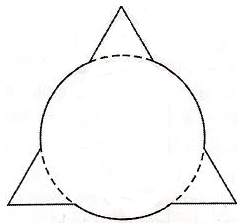
Sabendo-se que as duas figuras têm centros no mesmo ponto, pode-se afirmar que o perímetro do logotipo é, em cm, igual a:

a) 6(6-π)
b) 6(9-π)
c) 6(6+π)
d) 9(3+2π)
e) 9(2+3π)

Gabarito: letra "c".
Comentário:
Eu tentei fazer essa questão, mas a minha resposta não se encaixa nem no gabarito, observem:
Perímetro do triângulo = 3.18
Pt = 54 cm
Perímetro do círculo = 2πR
Pc = 12π
Perímetro da figura = 12π + 54 cm
Pf = 6(2π + 9)

Digitei errado esta frase. O correto é "No triângulo retângulo OPA, OÂP = 60º"
Vou editar em vermelho, na minha solução original.

Vou explicar com detalhes, porque o ângulo vale OÂP = 60º (e também OÊP = 60º):

Seja V o vértice superior do triângulo ---> VP = altura do triângulo

VP = VM.cos30º ---> VP = 18.(√3/2) ---> VP = 9.√3

Como O é o baricentro do triângulo ---> OV = 2.OP --->

OV + OP = VP ---> 2.OP + OP = 9.√3  ---> OP = 3.√3  

No triângulo retângulo OPA ---> 

sen(OÂP) = OP/OA ---> sen(OÂP) = 3.√3/6 ---> sen(OÂP) = √3/2 ---> OÂP = 60º

Do mesmo modo OÊP = 60º